


Next: Jupiter
Up: The Superior Planets
Previous: Mars
Figure 32 shows the geocentric orbit of a superior planet. Recall that the vector 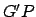 is always parallel to the vector connecting the earth to the sun. It follows that
a so-called conjunction, at which the sun lies
directly between the planet and the earth, occurs whenever the epicyclic anomaly,
is always parallel to the vector connecting the earth to the sun. It follows that
a so-called conjunction, at which the sun lies
directly between the planet and the earth, occurs whenever the epicyclic anomaly, 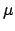 , takes the value
, takes the value 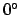 . At
a conjunction, the planet is furthest from the earth, and has the same ecliptic longitude as the
sun, and is, therefore, invisible. Conversely, a so-called opposition, at which the earth lies directly between the planet and the sun, occurs whenever
. At
a conjunction, the planet is furthest from the earth, and has the same ecliptic longitude as the
sun, and is, therefore, invisible. Conversely, a so-called opposition, at which the earth lies directly between the planet and the sun, occurs whenever 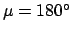 . At an opposition, the planet is closest to the earth, and also directly opposite the
sun in the sky, and, therefore, at its brightest. Now, a superior planet rotates around the epicycle at a
faster angular velocity than its guide-point rotates around the deferent. Moreover, both the planet and guide-point rotate
in the same direction. It follows that the planet is traveling backward in the sky (relative to the direction
of its mean motion) at opposition. This phenomenon is called retrograde motion. The period of
retrograde motion begins and ends at stations--so-called because when the planet reaches them
it appears to stand still in the sky for a few days whilst it reverses direction.
. At an opposition, the planet is closest to the earth, and also directly opposite the
sun in the sky, and, therefore, at its brightest. Now, a superior planet rotates around the epicycle at a
faster angular velocity than its guide-point rotates around the deferent. Moreover, both the planet and guide-point rotate
in the same direction. It follows that the planet is traveling backward in the sky (relative to the direction
of its mean motion) at opposition. This phenomenon is called retrograde motion. The period of
retrograde motion begins and ends at stations--so-called because when the planet reaches them
it appears to stand still in the sky for a few days whilst it reverses direction.
Tables 46-48 can be used to determine the dates of the conjunctions, oppositions, and
stations of Mars. Consider the first conjunction after the epoch (January 1, 2000 CE). We can estimate the
time at which this event occurs by approximating the epicyclic anomaly as the so-called
mean epicyclic anomaly:
We obtain
A calculation of the epicyclic anomaly at this time, using Tables 46-48, yields
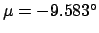 . Now, the
actual conjunction occurs when
. Now, the
actual conjunction occurs when 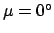 . Hence, our next estimate is
. Hence, our next estimate is
A
calculation of the epicyclic anomaly at this time gives 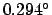 . Thus, our final estimate is
. Thus, our final estimate is
which corresponds to July 1, 2000 CE.
Consider the first opposition of Mars after the epoch. Our first estimate of the time at which this
event takes place is
A calculation of
the epicyclic anomaly at this time yields
 . Now, the actual
opposition occurs when
. Now, the actual
opposition occurs when 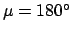 .
Hence, our second estimate is
.
Hence, our second estimate is
A calculation of the epicyclic anomaly
at this time gives  . Thus, our third estimate is
. Thus, our third estimate is
A calculation of the epicyclic anomaly at this time yields 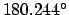 .
Hence, our final estimate is
.
Hence, our final estimate is
which corresponds to
June 13, 2001 CE. Incidentally, it is clear from the above analysis that the
mean time period between successive conjunctions, or oppositions, of Mars is
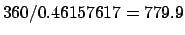 JD, which is
equivalent to
JD, which is
equivalent to 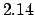 years.
years.
Let us now consider the stations of Mars. We can approximate the ecliptic longitude of a superior
planet
as
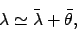 |
(184) |
where
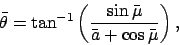 |
(185) |
and
 .
Note that
.
Note that
 and
and
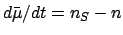 . It follows that
. It follows that
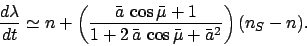 |
(186) |
Now, a station corresponds to
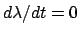 (i.e., a local maximum or minimum of
(i.e., a local maximum or minimum of 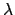 ), which gives
), which gives
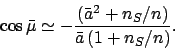 |
(187) |
For the case of Mars, we find that
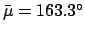 or
or 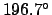 . The first solution corresponds
to the so-called retrograde station, at which the planet switches from direct to retrograde motion.
The second solution corresponds to the so-called direct station, at which the planet switches
from retrograde to direct motion. The mean time interval between a retrograde station and the following
opposition, or between an opposition and the following direct station, is
. The first solution corresponds
to the so-called retrograde station, at which the planet switches from direct to retrograde motion.
The second solution corresponds to the so-called direct station, at which the planet switches
from retrograde to direct motion. The mean time interval between a retrograde station and the following
opposition, or between an opposition and the following direct station, is
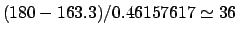 JD.
Unfortunately, the only option for accurately determining the dates at which the stations occur is to calculate
the ecliptic longitude of Mars over a range of days centered 36 days before and after its opposition.
JD.
Unfortunately, the only option for accurately determining the dates at which the stations occur is to calculate
the ecliptic longitude of Mars over a range of days centered 36 days before and after its opposition.
Table 49 shows the conjunctions, oppositions, and
stations of Mars for the years 2000-2020 CE, calculated using the
techniques described above.



Next: Jupiter
Up: The Superior Planets
Previous: Mars
Richard Fitzpatrick
2010-07-21