

Next: Mars
Up: Planetary Latitudes
Previous: Introduction
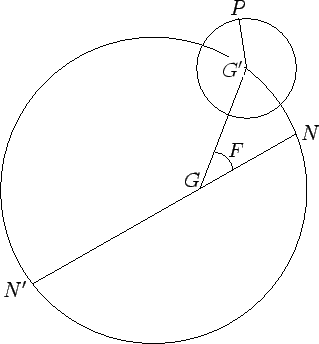
Figure 34 shows the orbit of a superior planet.
As we have already mentioned, the deferent and epicycle of such a planet have the same elements as
the orbit of the planet in question around the sun, and the apparent orbit of the
sun around the earth, respectively. It follows that the deferent and epicycle of a
superior planet are, respectively, inclined and parallel to the ecliptic plane.
(Recall that the ecliptic plane corresponds to the
plane of the sun's apparent orbit about the earth.) Let the plane of the deferent cut the
ecliptic plane along the line 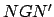 . Here,
. Here, 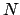 is the point at which the
deferent passes through the plane of the ecliptic from south to north, in the direction of the
mean planetary motion. This point is called the ascending node.
Note that the line
is the point at which the
deferent passes through the plane of the ecliptic from south to north, in the direction of the
mean planetary motion. This point is called the ascending node.
Note that the line 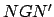 must pass through point
must pass through point 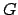 , since the
earth is common to the plane of the deferent and the ecliptic plane.
Now, it follows from simple geometry that the elevation of the guide-point
, since the
earth is common to the plane of the deferent and the ecliptic plane.
Now, it follows from simple geometry that the elevation of the guide-point 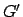 above of the
ecliptic plane satisfies
above of the
ecliptic plane satisfies
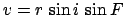 , where
, where 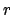 is the length
is the length 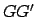 ,
, 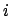 the fixed inclination of the
planetary orbit (and, hence, of the deferent) to the ecliptic plane, and
the fixed inclination of the
planetary orbit (and, hence, of the deferent) to the ecliptic plane, and 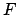 the angle
the angle 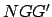 . The
angle
. The
angle 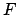 is termed the argument of latitude. We can write (see Cha. 8)
is termed the argument of latitude. We can write (see Cha. 8)
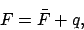 |
(205) |
where 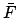 is the mean argument of latitude, and
is the mean argument of latitude, and 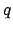 the equation of center of the deferent. Note that
the equation of center of the deferent. Note that 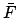 increases uniformly in time: i.e.,
increases uniformly in time: i.e.,
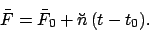 |
(206) |
Now, since the epicycle is parallel to the ecliptic
plane, the elevation of the planet above the said plane is
the same as that of the guide-point. Hence, from simple geometry, the ecliptic latitude of the planet satisfies
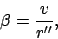 |
(207) |
where 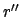 is the length
is the length 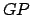 , and
we have used the small angle approximation. However, it is apparent from Fig. 31 that
, and
we have used the small angle approximation. However, it is apparent from Fig. 31 that
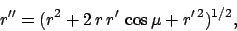 |
(208) |
where 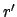 the length
the length 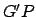 , and
, and 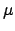 the
equation of the epicycle. But, according to the analysis in Cha. 8,
the
equation of the epicycle. But, according to the analysis in Cha. 8, 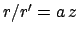 , where
, where 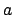 is the planetary
major radius in units in which the major radius of the sun's apparent orbit
about the earth is unity, and
is the planetary
major radius in units in which the major radius of the sun's apparent orbit
about the earth is unity, and 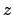 is defined in Eq. (158).
Thus, we obtain
is defined in Eq. (158).
Thus, we obtain
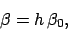 |
(209) |
where
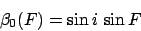 |
(210) |
is termed the deferential latitude,
and
![\begin{displaymath}
h(\mu,z) = \left[1 + 2\,(a\,z)^{-1}\,\cos\mu+ (a\,z)^{-2}\right]^{-1/2}
\end{displaymath}](img2023.png) |
(211) |
the epicyclic latitude correction factor.
Figure 34:
Orbit of a superior planet. Here, 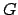 ,
, 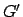 ,
, 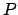 ,
,
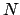 ,
, 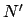 , and
, and 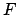 represent the earth, guide-point,
planet, ascending node, descending node, and argument of latitude, respectively. View is from northern
ecliptic pole.
represent the earth, guide-point,
planet, ascending node, descending node, and argument of latitude, respectively. View is from northern
ecliptic pole.
 |
In the following, 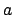 ,
, 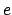 ,
, 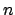 ,
, 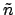 ,
, 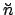 ,
,
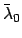 ,
, 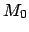 ,
, 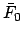 , and
, and 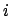 are elements of the orbit of the planet in question
about the sun, and
are elements of the orbit of the planet in question
about the sun, and 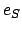 ,
, 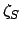 , and
, and 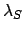 are elements of the sun's apparent orbit
about the earth.
The requisite elements for all of the superior planets at the J2000 epoch (
are elements of the sun's apparent orbit
about the earth.
The requisite elements for all of the superior planets at the J2000 epoch (
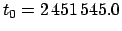 JD)
are listed in Tables 30 and 66.
Employing a quadratic interpolation scheme to represent
JD)
are listed in Tables 30 and 66.
Employing a quadratic interpolation scheme to represent
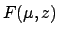 (see Cha. 8), our procedure for determining the ecliptic latitude of a
superior planet is summed up by the following formuale:
(see Cha. 8), our procedure for determining the ecliptic latitude of a
superior planet is summed up by the following formuale:
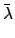 |
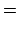 |
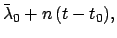 |
(212) |
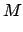 |
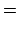 |
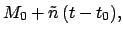 |
(213) |
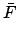 |
 |
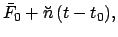 |
(214) |
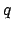 |
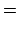 |
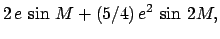 |
(215) |
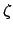 |
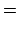 |
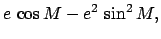 |
(216) |
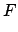 |
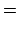 |
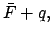 |
(217) |
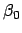 |
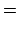 |
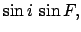 |
(218) |
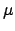 |
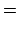 |
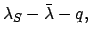 |
(219) |
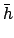 |
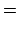 |
![$\displaystyle h(\mu,\bar{z})\equiv\left[1 + 2\,(a\,\bar{z})^{-1}\,\cos\mu+ (a\,\bar{z})^{-2}\right]^{-1/2},$](img2031.png) |
(220) |
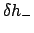 |
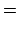 |
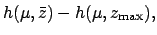 |
(221) |
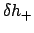 |
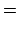 |
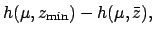 |
(222) |
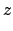 |
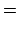 |
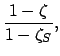 |
(223) |
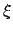 |
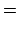 |
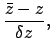 |
(224) |
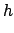 |
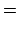 |
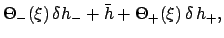 |
(225) |
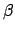 |
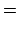 |
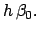 |
(226) |
Here,
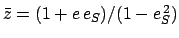 ,
,
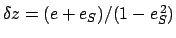 ,
,
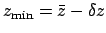 ,
and
,
and
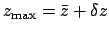 . The constants
. The constants 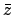 ,
, 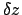 ,
, 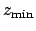 , and
, and 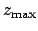 for each of the superior planets are listed in Table 44. Finally, the functions
for each of the superior planets are listed in Table 44. Finally, the functions 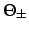 are tabulated in Table 45.
are tabulated in Table 45.
For the case of Mars, the above formulae are capable of matching NASA ephemeris data during the years 1995-2006 CE
with a mean error of 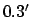 and a maximum error of
and a maximum error of 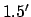 . For the case of Jupiter, the mean error is
. For the case of Jupiter, the mean error is
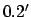 and the maximum error
and the maximum error 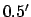 . Finally, for the case of Saturn, the mean error is
. Finally, for the case of Saturn, the mean error is 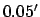 and the
maximum error
and the
maximum error 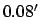 .
.


Next: Mars
Up: Planetary Latitudes
Previous: Introduction
Richard Fitzpatrick
2010-07-21

![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
, ![]() , and
, and ![]() are elements of the orbit of the planet in question
about the sun, and
are elements of the orbit of the planet in question
about the sun, and ![]() ,
, ![]() , and
, and ![]() are elements of the sun's apparent orbit
about the earth.
The requisite elements for all of the superior planets at the J2000 epoch (
are elements of the sun's apparent orbit
about the earth.
The requisite elements for all of the superior planets at the J2000 epoch (
![]() JD)
are listed in Tables 30 and 66.
Employing a quadratic interpolation scheme to represent
JD)
are listed in Tables 30 and 66.
Employing a quadratic interpolation scheme to represent
![]() (see Cha. 8), our procedure for determining the ecliptic latitude of a
superior planet is summed up by the following formuale:
(see Cha. 8), our procedure for determining the ecliptic latitude of a
superior planet is summed up by the following formuale:
![$\displaystyle h(\mu,\bar{z})\equiv\left[1 + 2\,(a\,\bar{z})^{-1}\,\cos\mu+ (a\,\bar{z})^{-2}\right]^{-1/2},$](img2031.png)
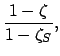
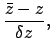
![]() and a maximum error of
and a maximum error of ![]() . For the case of Jupiter, the mean error is
. For the case of Jupiter, the mean error is
![]() and the maximum error
and the maximum error ![]() . Finally, for the case of Saturn, the mean error is
. Finally, for the case of Saturn, the mean error is ![]() and the
maximum error
and the
maximum error ![]() .
.