

Next: Saturn
Up: The Superior Planets
Previous: Determination of Conjunction, Opposition,
The ecliptic longitude of Jupiter can be determined with the aid of Tables 50-52. Table 50 allows
the mean longitude,  , and the mean anomaly,
, and the mean anomaly, 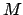 , of Jupiter to be calculated as functions of
time. Next, Table 51 permits the equation of center,
, of Jupiter to be calculated as functions of
time. Next, Table 51 permits the equation of center, 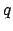 , and the radial anomaly,
, and the radial anomaly, 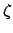 , to
be determined as functions of the mean anomaly. Finally, Table 52 allows the quantities
, to
be determined as functions of the mean anomaly. Finally, Table 52 allows the quantities
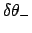 ,
, 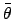 , and
, and
 to be calculated as functions of the epicyclic
anomaly,
to be calculated as functions of the epicyclic
anomaly,  .
The procedure for using the tables is analogous to the previously described procedure for
using the Mars tables.
One example of this procedure is given below.
.
The procedure for using the tables is analogous to the previously described procedure for
using the Mars tables.
One example of this procedure is given below.
Example: May 5, 2005 CE, 00:00 UT:
From before,
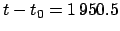 JD,
JD,
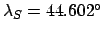 ,
,
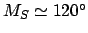 , and
, and
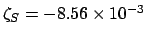 . Making use of
Table 50, we find:
. Making use of
Table 50, we find:
| |
|
|
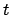 (JD) (JD) |
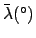 |
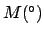 |
| |
|
|
| +1000 |
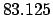 |
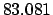 |
| +900 |
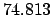 |
 |
| +50 |
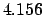 |
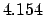 |
| +.5 |
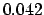 |
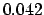 |
| Epoch |
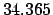 |
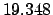 |
| |
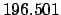 |
 |
| Modulus |
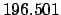 |
 |
| |
|
|
Given that
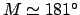 , Table 51 yields
, Table 51 yields
Thus,
where we have rounded the epicylic anomaly to the nearest degree. It follows from Table 52
that
Now,
However, from Table 44,
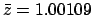 and
and
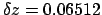 ,
so
,
so
According to Table 45,
so
Finally,
Thus,
the ecliptic longitude of Jupiter at 00:00 UT on May 5, 2005 CE was 10LI29.
The conjunctions, oppositions, and stations of Jupiter can be investigated
using analogous methods to those employed earlier to examine the
conjunctions, oppositions, and stations of Mars. We find that the mean
time period between successive oppositions or conjunctions of
Jupiter is 1.09 yr. Furthermore, on average, the retrograde and direct
stations of Jupiter occur when the epicyclic anomaly takes the
values
 and
and 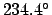 , respectively. Finally,
the mean time period between a retrograde station and the following
opposition, or between the opposition and the following direct
station, is 60 JD. The conjunctions, oppositions, and stations of Jupiter
during the years 2000-2010 CE are shown in Table 53.
, respectively. Finally,
the mean time period between a retrograde station and the following
opposition, or between the opposition and the following direct
station, is 60 JD. The conjunctions, oppositions, and stations of Jupiter
during the years 2000-2010 CE are shown in Table 53.


Next: Saturn
Up: The Superior Planets
Previous: Determination of Conjunction, Opposition,
Richard Fitzpatrick
2010-07-21
![]() JD,
JD,
![]() ,
,
![]() , and
, and
![]() . Making use of
Table 50, we find:
. Making use of
Table 50, we find:
![]() and
and ![]() , respectively. Finally,
the mean time period between a retrograde station and the following
opposition, or between the opposition and the following direct
station, is 60 JD. The conjunctions, oppositions, and stations of Jupiter
during the years 2000-2010 CE are shown in Table 53.
, respectively. Finally,
the mean time period between a retrograde station and the following
opposition, or between the opposition and the following direct
station, is 60 JD. The conjunctions, oppositions, and stations of Jupiter
during the years 2000-2010 CE are shown in Table 53.