Next: Determination of Lunar-Solar Elongation Up: Lunar-Solar Syzygies and Eclipses Previous: Lunar-Solar Syzygies and Eclipses

Introduction

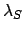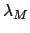Let $\lambda_S$ and $\lambda_M$ represent the ecliptic longitudes of the sun and the moon, respectively. The lunar-solar elongation is defined

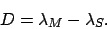$\begin{displaymath} D = \lambda_M - \lambda_S. \end{displaymath}$

(132)

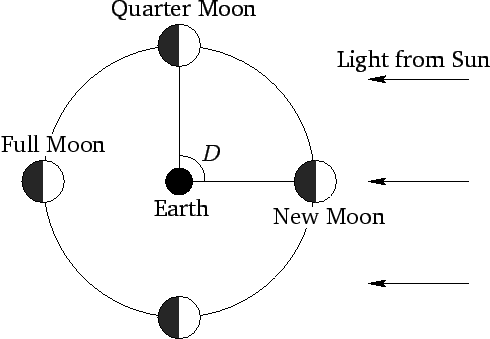
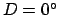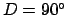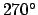Since the moon is only visible because of light reflected from the sun, there is a fairly obvious relationship between lunar-solar elongation and lunar phase--see Fig. 26. For instance, a new moon corresponds to $D = 0^\circ$ , a quarter moon to $D = 90^\circ$ or $270^\circ$ , and a full moon to 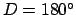$D = 180^\circ$ . New moons and full moons are collectively known as lunar-solar syzygies.

**Figure 26:** *The phases of the moon.*
$\begin{figure} \epsfysize =3in \centerline{\epsffile{epsfiles/phase.eps}} \end{figure}$

Richard Fitzpatrick 2010-07-21