Copernicus's Model of the Solar System

The Polish astronomer Nicolaus Copernicus (1473-1543 CE) studied the Almagest assiduously, but eventually became dissatisfied with Ptolomy's approach. The main reason for this dissatisfaction was not the geocentric nature of Ptolomy's model, but rather the fact that it mandates that heavenly bodies execute non-uniform circular motion. Copernicus, like Aristotle, was convinced that the supposed perfection of the heavens requires such bodies to execute uniform circular motion only. Copernicus was thus spurred to construct his own model of the solar system, which was described in the book De Revolutionibus Orbium Coelestium (On the Revolutions of the Heavenly Spheres), published in the year of his death.

The most well-known aspect of Copernicus's model is the fact that it is heliocentric. As has already been mentioned, when describing the motion of the sun, moon, and planets relative to the earth, it makes little practical difference whether one adopts a geocentric or a heliocentric model of the solar system. Having said this, the heliocentric approach does have one large advantage. If we accept that the sun, and not the earth, is stationary, then it immediately follows that the epicycles of the superior planets, and the deferents of the inferior planets, represent the earth's orbit around the sun. Hence, all of these circles must be the same size. This realization allows us to break the scale invariance which is one of the main failings of Ptolemy's model. Thus, the ratio of the deferent radius to that of the epicycle for a superior planet, which is easily inferred from observations, actually corresponds to the ratio of planet's orbital radius to that of the earth. Likewise, the ratio of the epicycle radius to that of the deferent for an inferior planet, which is again easily determined observationally, also corresponds to the ratio of the planet's orbital radius to that of the earth. Using this type of reasoning, Copernicus was able to construct the first accurate scale model of the solar system, and to firmly establish the order in which the planets orbit the sun. In some sense, this was his main achievement.

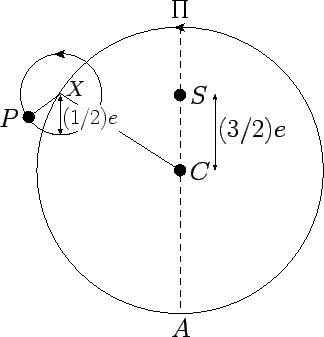
Copernicus's insistence that heavenly bodies should only move in uniform circles lead him to reject Ptolemy's equant scheme, and to replace it with the scheme illustrated in Fig. 2. According to Copernicus, a heliocentric planetary orbit is a combination of two circular motions. The first is motion of the planet around a small circular epicycle, and the second is the motion of the center of the epicycle around the sun on a circular deferent. Both motions are uniform, and in the same direction. However, the former motion is twice as fast as the latter. In addition, the sun is displaced from the center of the deferent in the direction of the perihelion, the displacement being proportional to the orbital eccentricity. Furthermore, the sun's displacement is three times greater than the radius of the epicycle. Finally, the radius of the deferent is equal to the major radius of the planetary orbit. It turns out that Copernicus' scheme is a marginally less accurate approximation than Ptolemy's to a low eccentricity Keplerian orbit (see Cha. 4).

Copernicus modeled the orbit of the earth around the sun using an Hippachian scheme (see Fig. 1) in which the earth moves uniformly around an eccentric circle. Unfortunately, such a scheme exaggerates the variation in the radial distance between the earth and the sun during the course of a year by a factor of $2$, and so introduces significant errors into the calculation of the parallax of the planets due to the motion of the earth. On the other hand, Copernicus' model of the moon's orbit around the earth is a considerable improvement on Ptolemy's, since it does not grossly exaggerate the monthly variation in the earth-moon distance. Like Ptolemy, Copernicus introduced an additional spurious epicycle into his model of Mercury's orbit, and erroneously allowed the inclination of his planetary orbits to vary slightly in time.

In summary, Copernicus's model of the solar system contains approximately the same number of epicycles as Ptolemy's, the only difference being that Copernicus' epicycles are much smaller than Ptolemy's. Indeed, the model of Copernicus is about as complicated, and not appreciably more accurate, than that described in the Almagest. In this respect, Copernicus cannot be said to have demonstrated the correctness of his heliocentric approach on the basis of observational data.

Figure 2: Copernicus' model of a heliocentric planetary orbit. Here, $S$ is the sun, $P$ the planet, $C$ the geometric center of the deferent, $X$ the center of the epicycle, $\Pi$ the perihelion, and $A$ the aphelion. The radius vectors $CX$ and $XP$ both rotate uniformly in the same direction, but $XP$ rotates twice as fast as $CX$. The major radius of the orbit is normalized to unity.