

Next: Equinoxes and Solstices
Up: Spherical Astronomy
Previous: Meridian Transits
According to Eq. (15), the sun's
declination varies between 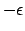 and
and 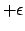 during the course of
a year.
It follows from Eq. (34) that it is only possible for the sun to have an
upper transit at the
zenith in a region of the earth whose
latitude lies between
during the course of
a year.
It follows from Eq. (34) that it is only possible for the sun to have an
upper transit at the
zenith in a region of the earth whose
latitude lies between 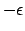 and
and  . The circles of latitude bounding this region are known
as the tropics. Thus, the tropic of Capricorn--so-called
because the sun is at the winter solstice, and, therefore, at the
first point of Capricorn (i.e., the zeroth degree of Capricorn), when it culminates at the
zenith at this latitude--lies at
. The circles of latitude bounding this region are known
as the tropics. Thus, the tropic of Capricorn--so-called
because the sun is at the winter solstice, and, therefore, at the
first point of Capricorn (i.e., the zeroth degree of Capricorn), when it culminates at the
zenith at this latitude--lies at
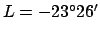 . Moreover,
the tropic of Cancer--so-called
because the sun is at the summer solstice, and, therefore, at the
first point of Cancer, when it culminates at the
zenith at this latitude--lies at
. Moreover,
the tropic of Cancer--so-called
because the sun is at the summer solstice, and, therefore, at the
first point of Cancer, when it culminates at the
zenith at this latitude--lies at
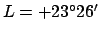 .
.
Equations (34) and (35) imply that the sun
does not rise for part of the year, and does not set for part of the year,
in two regions of the earth whose terrestrial latitudes satisfy
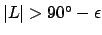 .
These two regions are bounded by the poles and two circles of latitude
known as the arctic circles. The
south arctic circle lies at
.
These two regions are bounded by the poles and two circles of latitude
known as the arctic circles. The
south arctic circle lies at
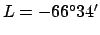 . Likewise,
the north arctic circle lies at
. Likewise,
the north arctic circle lies at
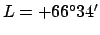 .
.
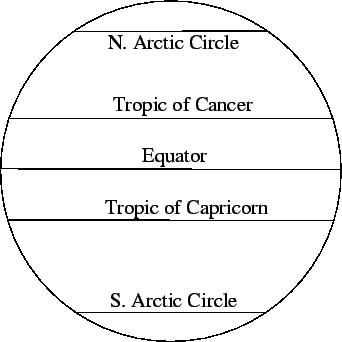
The equator, the two tropics, and the two arctic circles constitute the
five principal latitude circles of the earth, and are shown in Fig. 12.
Figure 12:
The principal latitude circles of the earth.
 |


Next: Equinoxes and Solstices
Up: Spherical Astronomy
Previous: Meridian Transits
Richard Fitzpatrick
2010-07-21
![]() .
These two regions are bounded by the poles and two circles of latitude
known as the arctic circles. The
south arctic circle lies at
.
These two regions are bounded by the poles and two circles of latitude
known as the arctic circles. The
south arctic circle lies at
![]() . Likewise,
the north arctic circle lies at
. Likewise,
the north arctic circle lies at
![]() .
.