Celestial Coordinates

Consider Fig. 3. The celestial sphere rotates about the celestial axis, $PP'$, which is the imagined extension of the earth's axis of rotation. This axis intersects the celestial sphere at the north celestial pole, $P$, and the south celestial pole, $P'$. It follows that the two celestial poles are unaffected by diurnal motion, and remain fixed in the sky.

Figure 3: The celestial sphere. $G$, $P$, $P'$, $V$, and $V'$ represent the earth, north celestial pole, south celestial pole, vernal equinox, and autumnal equinox, respectively. $VUV'U'$ is the celestial equator, and $PP'$ the celestial axis.

The celestial equator, $VUV'U'$, is the intersection of the earth's equatorial plane with the celestial sphere, and is therefore perpendicular to the celestial axis. The so-called vernal equinox, $V$, is a particular point on the celestial equator that is used as the origin of celestial longitude. Furthermore, the autumnal equinox, $V'$, is a point which lies directly opposite the vernal equinox on the celestial equator. Let the line $UU'$ lie in the plane of the celestial equator such that it is perpendicular to $VV'$, as shown in the figure.

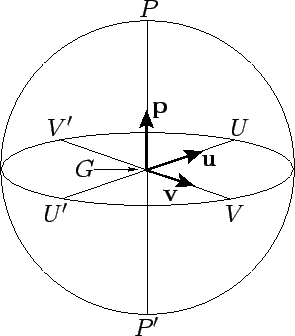
It is helpful to define three, right-handed, mutually perpendicular, unit vectors: ${\bf v}$, ${\bf u}$, and ${\bf p}$. Here, ${\bf v}$ is directed from the earth to the vernal equinox, ${\bf u}$ from the earth to point $U$, and ${\bf p}$ from the earth to the north celestial pole--see Fig. 3.

Figure 4: Celestial coordinates. $R$ is a celestial object, and $R'$ its projection onto the plane of the celestial equator, $VR'V'$.

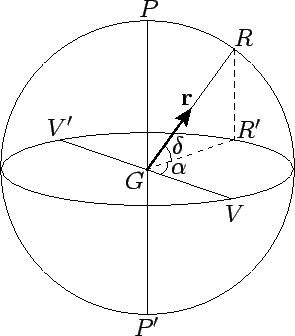Consider a general celestial object, $R$--see Fig. 4. The location of $R$ on the celestial sphere is conveniently specified by two angular coordinates, $\delta$ and $\alpha$. Let $GR'$ be the projection of $GR$ onto the equatorial plane. The coordinate $\delta$, which is known as declination, is the angle subtended between $GR'$ and $GR$. Objects north of the celestial equator have positive declinations, and vice versa. It follows that objects on the celestial equator have declinations of $0^\circ$, whereas the north and south celestial poles have declinations of $+90^\circ$ and $-90^\circ$, respectively. The coordinate $\alpha$, which is known as right ascension, is the angle subtended between $GV$ and $GR'$. Right ascension increases from west to east (i.e., in the opposite direction to the celestial sphere's diurnal rotation). Thus, the vernal and autumnal equinoxes have right ascensions of $0^\circ$ and $180^\circ$, respectively. Note that $\alpha$ lies in the range $0^\circ$ to $360^\circ$. Right ascension is sometimes measured in hours, instead of degrees, with one hour corresponding to $15^\circ$ (since it takes 24 hours for the celestial sphere to complete one diurnal rotation). In this scheme, the vernal and autumnal equinoxes have right ascensions of $0$ hrs. and $12$ hrs., respectively. Moreover, $\alpha$ lies in the range $0$ to 24 hrs. (Incidentally, in this treatise, $\alpha$ is measured relative to the mean equinox at date, unless otherwise specified.) Finally, let ${\bf r}$ be a unit vector which is directed from the earth to $R$--see Fig. 4. It is easily demonstrated that

$${\bf r} = \cos\delta\,\cos\alpha\,{\bf v} + \cos\delta\,\sin\alpha\,{\bf u} + \sin\delta\,{\bf p},$$ (1)

and

$$\sin\delta = {\bf r}\cdot {\bf p},$$ (2)

$$\tan\alpha = \left(\frac{{\bf r}\cdot{\bf u}}{{\bf r}\cdot {\bf v}}\right).$$ (3)