


Next: Photon statistics
Up: Quantum statistics
Previous: Formulation of the statistical
Fermi-Dirac statistics
Let us, first of all, consider Fermi-Dirac statistics. According to Eq. (582),
the average number of particles in quantum state 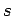 can be written
can be written
 |
(584) |
Here, we have rearranged the order of summation, using the multiplicative
properties of the exponential function. Note that the first sums in the
numerator and denominator
only involve 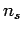 , whereas the last sums
omit the particular state
, whereas the last sums
omit the particular state 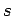 from consideration
(this is indicated by the superscript
from consideration
(this is indicated by the superscript 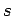 on the summation symbol). Of course,
the sums in the above expression range over all values of the
numbers
on the summation symbol). Of course,
the sums in the above expression range over all values of the
numbers
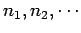 such that
such that 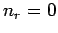 and 1 for
each
and 1 for
each 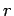 , subject to the overall constraint that
, subject to the overall constraint that
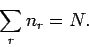 |
(585) |
Let us introduce the function
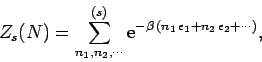 |
(586) |
which is defined as the partition function for  particles distributed over all
quantum states, excluding state
particles distributed over all
quantum states, excluding state 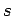 , according to Fermi-Dirac statistics.
By explicitly performing the sum over
, according to Fermi-Dirac statistics.
By explicitly performing the sum over 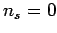 and 1, the
expression (584) reduces to
and 1, the
expression (584) reduces to
 |
(587) |
which yields
![\begin{displaymath}
\bar{n}_s =\frac{1}{[Z_s(N)/Z_s(N-1)]\,{\rm e}^{\,\beta\,\epsilon_s} + 1}.
\end{displaymath}](img1396.png) |
(588) |
In order to make further progress, we must somehow relate 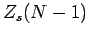 to
to
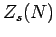 . Suppose that
. Suppose that
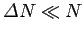 . It follows that
. It follows that
 can be Taylor expanded to give
can be Taylor expanded to give
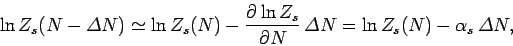 |
(589) |
where
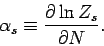 |
(590) |
As always, we Taylor expand the slowly varying function 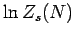 , rather
than the rapidly varying function
, rather
than the rapidly varying function 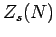 , because the radius of
convergence of the latter Taylor series is too small for the series to
be of any practical use. Equation (589) can be rearranged to give
, because the radius of
convergence of the latter Taylor series is too small for the series to
be of any practical use. Equation (589) can be rearranged to give
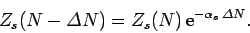 |
(591) |
Now, since 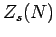 is a sum over very many
different quantum states, we would not expect the logarithm of this
function to be sensitive to which particular state
is a sum over very many
different quantum states, we would not expect the logarithm of this
function to be sensitive to which particular state 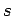 is excluded from consideration. Let us, therefore, introduce the
approximation that
is excluded from consideration. Let us, therefore, introduce the
approximation that 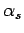 is independent of
is independent of 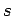 , so that we can write
, so that we can write
 |
(592) |
for all 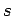 . It follows that the derivative (590) can be expressed
approximately in terms of the derivative of the full partition function
. It follows that the derivative (590) can be expressed
approximately in terms of the derivative of the full partition function
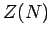 (in which the
(in which the  particles are distributed over
all quantum states). In fact,
particles are distributed over
all quantum states). In fact,
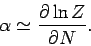 |
(593) |
Making use of Eq. (591), with
 , plus the
approximation (592), the expression (588) reduces to
, plus the
approximation (592), the expression (588) reduces to
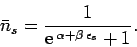 |
(594) |
This is called the Fermi-Dirac distribution. The parameter 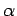 is determined by the constraint that
is determined by the constraint that
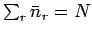 : i.e.,
: i.e.,
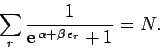 |
(595) |
Note that
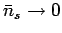 if
if 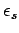 becomes sufficiently
large.
On the other hand, since the denominator in Eq. (594) can never become
less than unity, no matter how small
becomes sufficiently
large.
On the other hand, since the denominator in Eq. (594) can never become
less than unity, no matter how small 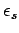 becomes, it follows
that
becomes, it follows
that
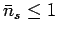 . Thus,
. Thus,
 |
(596) |
in accordance with the Pauli exclusion principle.
Equations (583) and (593) can be integrated to
give
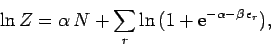 |
(597) |
where use has been made of Eq. (594).



Next: Photon statistics
Up: Quantum statistics
Previous: Formulation of the statistical
Richard Fitzpatrick
2006-02-02

![]() to
to
![]() . Suppose that
. Suppose that
![]() . It follows that
. It follows that
![]() can be Taylor expanded to give
can be Taylor expanded to give
![]() is a sum over very many
different quantum states, we would not expect the logarithm of this
function to be sensitive to which particular state
is a sum over very many
different quantum states, we would not expect the logarithm of this
function to be sensitive to which particular state ![]() is excluded from consideration. Let us, therefore, introduce the
approximation that
is excluded from consideration. Let us, therefore, introduce the
approximation that ![]() is independent of
is independent of ![]() , so that we can write
, so that we can write
![]() , plus the
approximation (592), the expression (588) reduces to
, plus the
approximation (592), the expression (588) reduces to
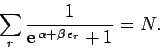
![]() if
if ![]() becomes sufficiently
large.
On the other hand, since the denominator in Eq. (594) can never become
less than unity, no matter how small
becomes sufficiently
large.
On the other hand, since the denominator in Eq. (594) can never become
less than unity, no matter how small ![]() becomes, it follows
that
becomes, it follows
that
![]() . Thus,
. Thus,