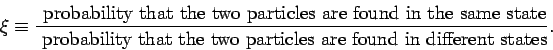An illustrative example

Consider a very simple gas made up of two identical particles. Suppose that each particle can be in one of three possible quantum states, 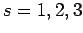$s=1,2,3$. Let us enumerate the possible states of the whole gas according to Maxwell-Boltzmann, Bose-Einstein, and Fermi-Dirac statistics, respectively.

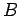For the case of Maxwell-Boltzmann (MB) statistics, the two particles are considered to be distinguishable. Let us denote them $A$ and $B$. Furthermore, any number of particles can occupy the same quantum state. The possible different states of the gas are shown in Tab. 6.

Table 6: Two particles distributed amongst three states according to Maxwell-Boltzmann statistics.

1	2	3
$AB$	$\cdots$	$\cdots$
$\cdots$	$AB$	$\cdots$
$\cdots$	$\cdots$	$AB$
$A$	$B$	$\cdots$
$B$	$A$	$\cdots$
$A$	$\cdots$	$B$
$B$	$\cdots$	$A$
$\cdots$	$A$	$B$
$\cdots$	$B$	$A$

There are clearly 9 distinct states.

For the case of Bose-Einstein (BE) statistics, the two particles are considered to be indistinguishable. Let us denote them both as $A$. Furthermore, any number of particles can occupy the same quantum state. The possible different states of the gas are shown in Tab. 7.

Table 7: Two particles distributed amongst three states according to Bose-Einstein statistics.

1	2	3
$AA$	$\cdots$	$\cdots$
$\cdots$	$AA$	$\cdots$
$\cdots$	$\cdots$	$AA$
$A$	$A$	$\cdots$
$A$	$\cdots$	$A$
$\cdots$	$A$	$A$

There are clearly 6 distinct states.

Finally, for the case of Fermi-Dirac (FD) statistics, the two particles are considered to be indistinguishable. Let us again denote them both as $A$. Furthermore, no more than one particle can occupy a given quantum state. The possible different states of the gas are shown in Tab. 8.

Table 8: Two particles distributed amongst three states according to Fermi-Dirac statistics.

1	2	3
$A$	$A$	$\cdots$
$A$	$\cdots$	$A$
$\cdots$	$A$	$A$

There are clearly only 3 distinct states.

It follows, from the above example, that Fermi-Dirac statistics are more restrictive (i.e., there are less possible states of the system) than Bose-Einstein statistics, which are, in turn, more restrictive than Maxwell-Boltzmann statistics. Let

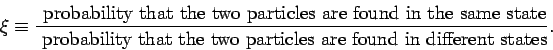$$\xi \equiv \frac{\mbox{ probability that the two particles a... ...bility that the two particles are found in different states}}.$$ (575)

For the case under investigation,

$$\xi_{\rm MB} = 1/2,$$ (576)

$$\xi_{\rm BE} = 1,$$ (577)

$$\xi_{\rm FD} = 0.$$ (578)

We conclude that in Bose-Einstein statistics there is a greater relative tendency for particles to cluster in the same state than in classical statistics. On the other hand, in Fermi-Dirac statistics there is less tendency for particles to cluster in the same state than in classical statistics.