


Next: Reversibility and irreversibility
Up: Statistical mechanics
Previous: The theorem
The relaxation time
The 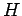 theorem guarantees that an isolated many particle system will eventually
reach equilibrium, irrespective of its initial state.
The typical time-scale for this process
is called the relaxation time, and depends in detail on the nature
of the
inter-particle interactions. The principle of equal a priori probabilities is
only valid for equilibrium states. It follows that we can only safely apply this
principle to systems which have remained undisturbed for many relaxation times
since they were setup, or last interacted with the outside world.
The relaxation time for the air in a typical classroom is
very much less than one second. This suggests that such air is probably in
equilibrium most of the time, and should, therefore, be governed by the
principle of equal a priori probabilities. In fact, this is known
to be the case. Consider another example. Our galaxy, the ``Milky Way,'' is
an isolated dynamical system made up of about
theorem guarantees that an isolated many particle system will eventually
reach equilibrium, irrespective of its initial state.
The typical time-scale for this process
is called the relaxation time, and depends in detail on the nature
of the
inter-particle interactions. The principle of equal a priori probabilities is
only valid for equilibrium states. It follows that we can only safely apply this
principle to systems which have remained undisturbed for many relaxation times
since they were setup, or last interacted with the outside world.
The relaxation time for the air in a typical classroom is
very much less than one second. This suggests that such air is probably in
equilibrium most of the time, and should, therefore, be governed by the
principle of equal a priori probabilities. In fact, this is known
to be the case. Consider another example. Our galaxy, the ``Milky Way,'' is
an isolated dynamical system made up of about 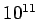 stars. In fact,
it can be thought
of as a self-gravitating ``gas'' of stars. At first sight, the
``Milky Way''
would seem to be an ideal system on which
to test out the ideas of statistical mechanics.
Stars in the Galaxy interact via occasional ``near miss'' events in which they
exchange energy and momentum. Actual collisions are very rare indeed. Unfortunately,
such interactions take place very infrequently, because
there is an awful lot of empty space between stars. The best estimate for the
relaxation time of the ``Milky Way'' is about
stars. In fact,
it can be thought
of as a self-gravitating ``gas'' of stars. At first sight, the
``Milky Way''
would seem to be an ideal system on which
to test out the ideas of statistical mechanics.
Stars in the Galaxy interact via occasional ``near miss'' events in which they
exchange energy and momentum. Actual collisions are very rare indeed. Unfortunately,
such interactions take place very infrequently, because
there is an awful lot of empty space between stars. The best estimate for the
relaxation time of the ``Milky Way'' is about 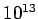 years.
This should be compared with the estimated age of the Galaxy, which is only
about
years.
This should be compared with the estimated age of the Galaxy, which is only
about 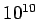 years. It is clear that, despite its great age, the ``Milky Way''
has not been around long enough to reach an equilibrium
state. This suggests that
the principle of equal a priori probabilities cannot be used to
describe stellar dynamics. Not surprisingly, the observed velocity distribution
of the stars in the vicinity of the Sun is not governed by this principle.
years. It is clear that, despite its great age, the ``Milky Way''
has not been around long enough to reach an equilibrium
state. This suggests that
the principle of equal a priori probabilities cannot be used to
describe stellar dynamics. Not surprisingly, the observed velocity distribution
of the stars in the vicinity of the Sun is not governed by this principle.



Next: Reversibility and irreversibility
Up: Statistical mechanics
Previous: The theorem
Richard Fitzpatrick
2006-02-02