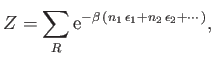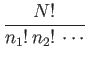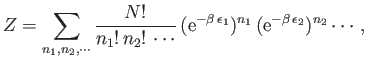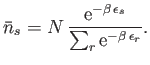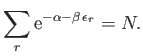Next: Quantum Statistics in Classical
Up: Quantum Statistics
Previous: Bose-Einstein Statistics
For the purpose of comparison, it is instructive to consider the purely
classical case of Maxwell-Boltzmann statistics. The partition
function is written
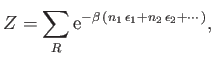 |
(8.46) |
where the sum is over all distinct states 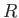 of the gas, and the particles
are treated as distinguishable. For given values of
of the gas, and the particles
are treated as distinguishable. For given values of
 there
are
there
are
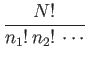 |
(8.47) |
possible ways in which  distinguishable
particles can be put into individual quantum states such that there are
distinguishable
particles can be put into individual quantum states such that there are  particles in state 1,
particles in state 1, 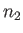 particles in state 2, et cetera. Each of these possible
arrangements corresponds to a distinct state for the whole gas.
Hence, Equation (8.46) can be written
particles in state 2, et cetera. Each of these possible
arrangements corresponds to a distinct state for the whole gas.
Hence, Equation (8.46) can be written
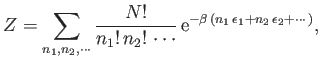 |
(8.48) |
where the sum is over all values of
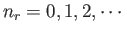 for each
for each  , subject to
the constraint that
, subject to
the constraint that
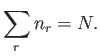 |
(8.49) |
Now, Equation (8.48) can be written
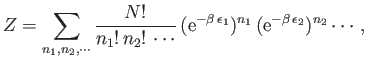 |
(8.50) |
which, by virtue of Equation (8.49), is just the result of
expanding a polynomial. In fact,
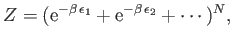 |
(8.51) |
or
 |
(8.52) |
Note that the argument of the logarithm is simply the single-particle partition function
Equations (8.20) and (8.52) can be combined to give
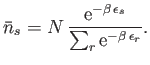 |
(8.53) |
This is known as the Maxwell-Boltzmann distribution. It is, of course,
just the result obtained by applying the canonical distribution to a single
particle. (See Chapter 7.) The previous expression can also be written
in the form
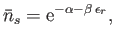 |
(8.54) |
where
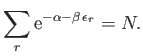 |
(8.55) |
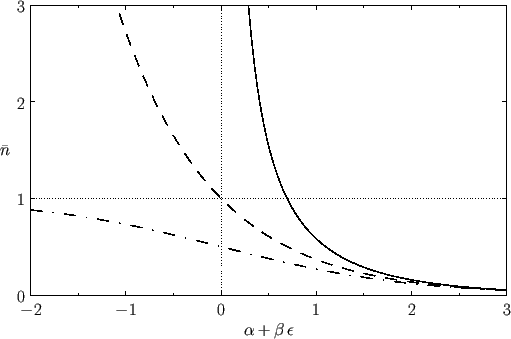
The Bose-Einstein, Maxwell-Boltzmann, and Fermi-Dirac distributions are illustrated in Figure 8.1.
Figure 8.1:
A comparison of the Bose-Einstein (solid curve), Maxwell-Boltzmann (dashed curve), and
Fermi-Dirac (dash-dotted curve) distributions.
 |



Next: Quantum Statistics in Classical
Up: Quantum Statistics
Previous: Bose-Einstein Statistics
Richard Fitzpatrick
2016-01-25