


Next: Maxwell-Boltzmann Statistics
Up: Quantum Statistics
Previous: Photon Statistics
Let us now consider Bose-Einstein statistics. The particles in the
system are assumed to be massive, so the total number of
particles,  , is a fixed number.
, is a fixed number.
Consider the expression (8.21). For the case of massive bosons, the numbers
 assume all values
assume all values
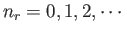 for each
for each  , subject to
the constraint that
, subject to
the constraint that
 .
Performing explicitly the sum over
.
Performing explicitly the sum over 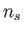 , this expression reduces to
, this expression reduces to
 |
(8.41) |
where 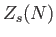 is the partition function for
is the partition function for  particles
distributed over all quantum states, excluding state
particles
distributed over all quantum states, excluding state  , according
to Bose-Einstein statistics [cf., Equation (8.23)]. Using Equation (8.28),
and the approximation (8.29), the previous equation reduces to
, according
to Bose-Einstein statistics [cf., Equation (8.23)]. Using Equation (8.28),
and the approximation (8.29), the previous equation reduces to
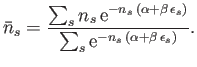 |
(8.42) |
Note that this expression is identical to (8.35), except that
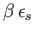 is replaced by
is replaced by
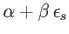 . Hence,
an analogous calculation to that outlined in the previous section yields
. Hence,
an analogous calculation to that outlined in the previous section yields
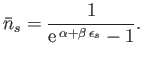 |
(8.43) |
This is called the Bose-Einstein distribution. Note that 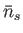 can become very large in this distribution. The parameter
can become very large in this distribution. The parameter 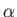 is again determined
by the constraint on the total number of particles: that is,
is again determined
by the constraint on the total number of particles: that is,
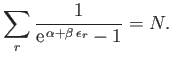 |
(8.44) |
Equations (8.20) and (8.30) can be integrated to
give
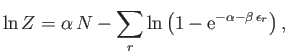 |
(8.45) |
where use has been made of Equation (8.43).
Note that photon statistics correspond to the special case of Bose-Einstein
statistics in which the parameter 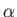 takes the value zero, and the constraint
(8.44) does not apply.
takes the value zero, and the constraint
(8.44) does not apply.



Next: Maxwell-Boltzmann Statistics
Up: Quantum Statistics
Previous: Photon Statistics
Richard Fitzpatrick
2016-01-25
![]() assume all values
assume all values
![]() for each
for each ![]() , subject to
the constraint that
, subject to
the constraint that
![]() .
Performing explicitly the sum over
.
Performing explicitly the sum over ![]() , this expression reduces to
, this expression reduces to

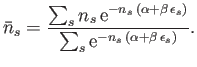
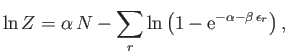
![]() takes the value zero, and the constraint
(8.44) does not apply.
takes the value zero, and the constraint
(8.44) does not apply.