


Next: Fermi-Dirac Statistics
Up: Quantum Statistics
Previous: Illustrative Example
Consider a gas consisting of  identical non-interacting particles
occupying volume
identical non-interacting particles
occupying volume  , and in thermal equilibrium at absolute temperature
, and in thermal equilibrium at absolute temperature  .
Let us label the possible quantum states of a single particle by
.
Let us label the possible quantum states of a single particle by  (or
(or  ).
Let the energy of a particle in state
).
Let the energy of a particle in state  be denoted
be denoted
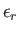 .
Let the number of particles in state
.
Let the number of particles in state  be written
be written 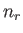 . Finally,
let us label the possible quantum states of the whole gas by
. Finally,
let us label the possible quantum states of the whole gas by 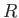 .
.
The particles are assumed to be non-interacting, so the
total energy of the gas in state 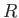 , where there are
, where there are 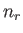 particles
in quantum state
particles
in quantum state  , et cetera, is simply
, et cetera, is simply
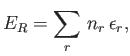 |
(8.16) |
where the sum extends over all possible quantum states,  . Furthermore,
because the total number of particles in the gas is known to be
. Furthermore,
because the total number of particles in the gas is known to be  , we must
have
, we must
have
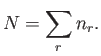 |
(8.17) |
In order to calculate the thermodynamic properties of the gas (i.e.,
its internal energy or its entropy), it is necessary to
calculate its partition function,
 |
(8.18) |
Here, the sum is over all possible states, 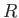 , of the whole gas.
That is, over all the various possible values of the
numbers
, of the whole gas.
That is, over all the various possible values of the
numbers
 .
.
Now,
![$ \exp[-\beta (n_1 \epsilon_1+n_2 \epsilon_2+\cdots)]$](img2021.png) is
the relative probability of finding the gas in a particular state in which
there are
is
the relative probability of finding the gas in a particular state in which
there are  particles in state 1,
particles in state 1, 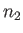 particles in state 2, et cetera.
Thus, the mean number of particles in quantum state
particles in state 2, et cetera.
Thus, the mean number of particles in quantum state  can be written
can be written
![$\displaystyle \bar{n}_s = \frac{\sum_R n_s \exp[-\beta (n_1 \epsilon_1+n_2 ...
...on_2+\cdots)]} {\sum_R \exp[-\beta (n_1 \epsilon_1+n_2 \epsilon_2+\cdots)]}.$](img2022.png) |
(8.19) |
A comparison of Equations (8.18) and (8.19) yields the result
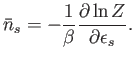 |
(8.20) |
Here,
 .
.



Next: Fermi-Dirac Statistics
Up: Quantum Statistics
Previous: Illustrative Example
Richard Fitzpatrick
2016-01-25
![]() , where there are
, where there are ![]() particles
in quantum state
particles
in quantum state ![]() , et cetera, is simply
, et cetera, is simply
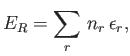
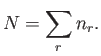
![]() is
the relative probability of finding the gas in a particular state in which
there are
is
the relative probability of finding the gas in a particular state in which
there are ![]() particles in state 1,
particles in state 1, ![]() particles in state 2, et cetera.
Thus, the mean number of particles in quantum state
particles in state 2, et cetera.
Thus, the mean number of particles in quantum state ![]() can be written
can be written