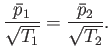Next: Ferromagnetism
Up: Applications of Statistical Thermodynamics
Previous: Maxwell Velocity Distribution
Effusion
Consider a dilute gas enclosed in a container. Let us calculate how many molecules per unit time strike a unit area of
the container wall.
Consider a wall element of area  . The
. The 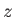 -axis is oriented so as to point along the outward
normal of this element. Let
-axis is oriented so as to point along the outward
normal of this element. Let 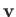 represent a molecular velocity.
The Cartesian components of this velocity are conveniently written
represent a molecular velocity.
The Cartesian components of this velocity are conveniently written
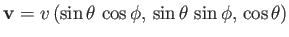 ,
where the standard spherical angles
,
where the standard spherical angles 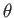 and
and 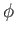 specify the velocity vector's direction.
Let us concentrate on those molecules, in the immediate vicinity of the wall element, whose velocities
are such that they lie between
specify the velocity vector's direction.
Let us concentrate on those molecules, in the immediate vicinity of the wall element, whose velocities
are such that they lie between 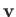 and
and
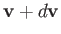 . In other words, the velocities are
such that their magnitudes lies between
. In other words, the velocities are
such that their magnitudes lies between  and
and 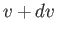 , their polar angles lie between
, their polar angles lie between
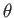 and
and
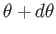 , and their azimuthal angles lie between
, and their azimuthal angles lie between 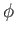 and
and
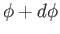 . Molecules of this type
suffer a displacement
. Molecules of this type
suffer a displacement
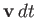 in the infinitesimal time interval
in the infinitesimal time interval 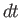 .
Hence, all molecules that lie within the infinitesimal cylinder of cross-sectional
area
.
Hence, all molecules that lie within the infinitesimal cylinder of cross-sectional
area  , and length
, and length
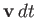 (whose axis subtends an angle
(whose axis subtends an angle 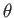 with the
with the 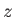 -axis, and whose two ends are parallel to the wall element),
will strike the wall element within the time interval
-axis, and whose two ends are parallel to the wall element),
will strike the wall element within the time interval 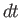 , whereas those
molecules outside this cylinder will not. (See Figure 7.8.) The volume of the cylinder is
, whereas those
molecules outside this cylinder will not. (See Figure 7.8.) The volume of the cylinder is
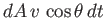 , whereas the
number of molecules per unit volume in the prescribed velocity range is
, whereas the
number of molecules per unit volume in the prescribed velocity range is
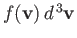 .
Hence, the number of molecules of this type that
strike the area
.
Hence, the number of molecules of this type that
strike the area  in the time interval
in the time interval 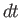 is
is
![$ [f({\bf v}) d^{ 3}{\bf v}] (dA v \cos\theta dt)$](img1756.png) .
Dividing this expression by the area
.
Dividing this expression by the area  , and the time interval
, and the time interval 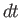 , we obtain
, we obtain
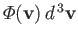 ,
which is defined as the number of molecules, with velocities in the range
,
which is defined as the number of molecules, with velocities in the range 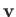 to
to
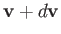 , that
strike a unit area of the wall per unit time. Thus,
, that
strike a unit area of the wall per unit time. Thus,
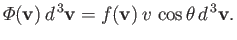 |
(7.233) |
Figure:
All molecules with velocity 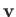 that lie within the cylinder strike the wall in a unit time interval.
that lie within the cylinder strike the wall in a unit time interval.
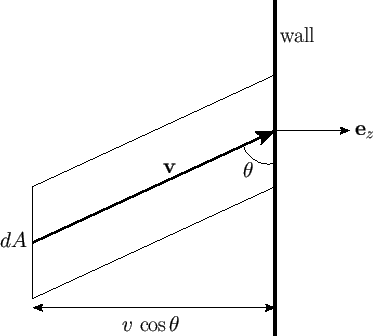 |
Let
 be the total number of molecules that strike a unit area of the wall per unit time.
This quantity is simply obtained by summing (7.233) over all possible molecular velocities that would cause molecules to collide with the element of area. This means that we
have to sum over all possible speeds,
be the total number of molecules that strike a unit area of the wall per unit time.
This quantity is simply obtained by summing (7.233) over all possible molecular velocities that would cause molecules to collide with the element of area. This means that we
have to sum over all possible speeds,
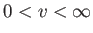 , all possible azimuthal angles,
, all possible azimuthal angles,
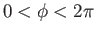 , and
all polar angles in the range
, and
all polar angles in the range
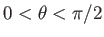 . (Those molecules with polar angles in the range
. (Those molecules with polar angles in the range
 have their velocity
directed away from the wall, and will, hence, not collide with it.) In other words, we have to
sum over all possible velocities,
have their velocity
directed away from the wall, and will, hence, not collide with it.) In other words, we have to
sum over all possible velocities, 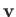 , subject to the restriction that the velocity component
, subject to the restriction that the velocity component
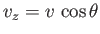 is positive. Thus, we have
is positive. Thus, we have
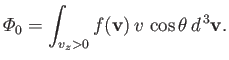 |
(7.234) |
The element of volume in velocity space can be expressed in spherical coordinates:
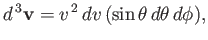 |
(7.235) |
where
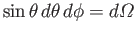 is just an element of solid angle.
Moreover, in thermal equilibrium,
is just an element of solid angle.
Moreover, in thermal equilibrium,
 is only a function of
is only a function of  .
Hence, Equation (7.234) becomes
.
Hence, Equation (7.234) becomes
The integral over 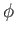 gives
gives 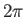 , whereas that over
, whereas that over 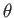 reduces to
reduces to 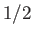 . It follows that
. It follows that
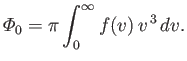 |
(7.237) |
Now, the mean molecular speed is written
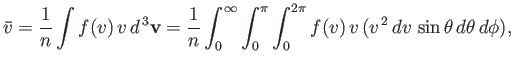 |
(7.238) |
which reduces to
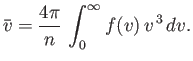 |
(7.239) |
Hence, we deduce from Equation (7.237) that
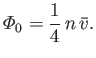 |
(7.240) |
The previous result can be combined with Equation (7.227), and the ideal equation of state,
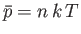 , to give
, to give
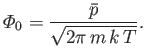 |
(7.241) |
If a sufficiently small hole is made in the wall of the container then the equilibrium of the gas inside the container is
disturbed to a negligible extent. [In practice, a sufficiently small hole is one that is small compared to the molecular mean-free-path (i.e., the
mean distance travelled between collisions) inside the container.] In this case, the number of molecules that emerge through the small hole is the same as
the number of molecules that would strike the area occupied by the hole if the latter were closed off. The process
by which molecules emerge through a small hole is called effusion. The number
of molecules that have speeds in the range between  and
and 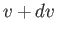 , and which emerge through a small hole
of area
, and which emerge through a small hole
of area  , into the solid angle range
, into the solid angle range
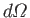 , in the forward direction
, in the forward direction 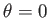 , is given by
, is given by
Now, it is difficult to directly verify the Maxwell velocity distribution. However, this
distribution can be verified indirectly by measuring the velocity distribution
of atoms effusing from a small hole in an oven. As we have just seen, the predicted velocity distribution of
the escaping atoms varies like
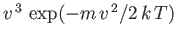 , in contrast
to the
, in contrast
to the
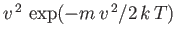 variation of the velocity distribution
inside the oven. There is good agreement between the experimentally measured velocity distribution of
effusing atoms and the theoretical prediction.
variation of the velocity distribution
inside the oven. There is good agreement between the experimentally measured velocity distribution of
effusing atoms and the theoretical prediction.
As another example, consider a container that is divided into two parts by a partition containing a small hole.
The container is filled with gas, but one part of the container is maintained at the temperature  , and the other
at the temperature
, and the other
at the temperature 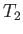 . Let us calculate the relationship between the mean gas pressures,
. Let us calculate the relationship between the mean gas pressures,  and
and 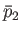 ,
respectively, in the two parts, when the system is in equilibrium. (That is, when a situation is reached in which
neither
,
respectively, in the two parts, when the system is in equilibrium. (That is, when a situation is reached in which
neither  or
or 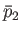 , nor the amount of gas in either parts, changes with time.) If the hole is
larger than the molecular mean-free-path then the relationship is simply
, nor the amount of gas in either parts, changes with time.) If the hole is
larger than the molecular mean-free-path then the relationship is simply
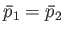 --otherwise, the
pressure difference would give rise to bulk motion of the gas from one side of the container to the other,
until the pressures were equalized. But, if the dimensions of the hole are less than the mean-free-path then we are
dealing with effusion through the hole, rather than hydrodynamical flow. In this case, the equilibrium
condition requires that the mass of gas on each side remain constant. In other words, the effusion rates in
both directions must be equal. Thus, it follows from Equation (7.241) that
--otherwise, the
pressure difference would give rise to bulk motion of the gas from one side of the container to the other,
until the pressures were equalized. But, if the dimensions of the hole are less than the mean-free-path then we are
dealing with effusion through the hole, rather than hydrodynamical flow. In this case, the equilibrium
condition requires that the mass of gas on each side remain constant. In other words, the effusion rates in
both directions must be equal. Thus, it follows from Equation (7.241) that
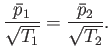 |
(7.243) |
Thus, the pressures are not equal. Instead, a higher pressure prevails in the part of the container held at a higher temperature.



Next: Ferromagnetism
Up: Applications of Statistical Thermodynamics
Previous: Maxwell Velocity Distribution
Richard Fitzpatrick
2016-01-25
![]() . The
. The ![]() -axis is oriented so as to point along the outward
normal of this element. Let
-axis is oriented so as to point along the outward
normal of this element. Let ![]() represent a molecular velocity.
The Cartesian components of this velocity are conveniently written
represent a molecular velocity.
The Cartesian components of this velocity are conveniently written
![]() ,
where the standard spherical angles
,
where the standard spherical angles ![]() and
and ![]() specify the velocity vector's direction.
Let us concentrate on those molecules, in the immediate vicinity of the wall element, whose velocities
are such that they lie between
specify the velocity vector's direction.
Let us concentrate on those molecules, in the immediate vicinity of the wall element, whose velocities
are such that they lie between ![]() and
and
![]() . In other words, the velocities are
such that their magnitudes lies between
. In other words, the velocities are
such that their magnitudes lies between ![]() and
and ![]() , their polar angles lie between
, their polar angles lie between
![]() and
and
![]() , and their azimuthal angles lie between
, and their azimuthal angles lie between ![]() and
and
![]() . Molecules of this type
suffer a displacement
. Molecules of this type
suffer a displacement
![]() in the infinitesimal time interval
in the infinitesimal time interval ![]() .
Hence, all molecules that lie within the infinitesimal cylinder of cross-sectional
area
.
Hence, all molecules that lie within the infinitesimal cylinder of cross-sectional
area ![]() , and length
, and length
![]() (whose axis subtends an angle
(whose axis subtends an angle ![]() with the
with the ![]() -axis, and whose two ends are parallel to the wall element),
will strike the wall element within the time interval
-axis, and whose two ends are parallel to the wall element),
will strike the wall element within the time interval ![]() , whereas those
molecules outside this cylinder will not. (See Figure 7.8.) The volume of the cylinder is
, whereas those
molecules outside this cylinder will not. (See Figure 7.8.) The volume of the cylinder is
![]() , whereas the
number of molecules per unit volume in the prescribed velocity range is
, whereas the
number of molecules per unit volume in the prescribed velocity range is
![]() .
Hence, the number of molecules of this type that
strike the area
.
Hence, the number of molecules of this type that
strike the area ![]() in the time interval
in the time interval ![]() is
is
![]() .
Dividing this expression by the area
.
Dividing this expression by the area ![]() , and the time interval
, and the time interval ![]() , we obtain
, we obtain
![]() ,
which is defined as the number of molecules, with velocities in the range
,
which is defined as the number of molecules, with velocities in the range ![]() to
to
![]() , that
strike a unit area of the wall per unit time. Thus,
, that
strike a unit area of the wall per unit time. Thus,

![]() be the total number of molecules that strike a unit area of the wall per unit time.
This quantity is simply obtained by summing (7.233) over all possible molecular velocities that would cause molecules to collide with the element of area. This means that we
have to sum over all possible speeds,
be the total number of molecules that strike a unit area of the wall per unit time.
This quantity is simply obtained by summing (7.233) over all possible molecular velocities that would cause molecules to collide with the element of area. This means that we
have to sum over all possible speeds,
![]() , all possible azimuthal angles,
, all possible azimuthal angles,
![]() , and
all polar angles in the range
, and
all polar angles in the range
![]() . (Those molecules with polar angles in the range
. (Those molecules with polar angles in the range
![]() have their velocity
directed away from the wall, and will, hence, not collide with it.) In other words, we have to
sum over all possible velocities,
have their velocity
directed away from the wall, and will, hence, not collide with it.) In other words, we have to
sum over all possible velocities, ![]() , subject to the restriction that the velocity component
, subject to the restriction that the velocity component
![]() is positive. Thus, we have
is positive. Thus, we have
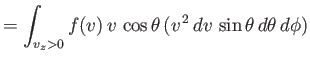
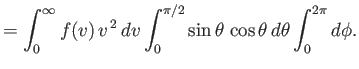
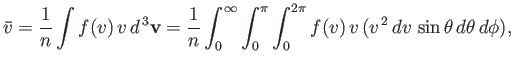
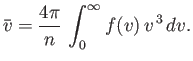
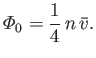
![]() and
and ![]() , and which emerge through a small hole
of area
, and which emerge through a small hole
of area ![]() , into the solid angle range
, into the solid angle range
![]() , in the forward direction
, in the forward direction ![]() , is given by
, is given by
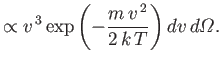
![]() , and the other
at the temperature
, and the other
at the temperature ![]() . Let us calculate the relationship between the mean gas pressures,
. Let us calculate the relationship between the mean gas pressures, ![]() and
and ![]() ,
respectively, in the two parts, when the system is in equilibrium. (That is, when a situation is reached in which
neither
,
respectively, in the two parts, when the system is in equilibrium. (That is, when a situation is reached in which
neither ![]() or
or ![]() , nor the amount of gas in either parts, changes with time.) If the hole is
larger than the molecular mean-free-path then the relationship is simply
, nor the amount of gas in either parts, changes with time.) If the hole is
larger than the molecular mean-free-path then the relationship is simply
![]() --otherwise, the
pressure difference would give rise to bulk motion of the gas from one side of the container to the other,
until the pressures were equalized. But, if the dimensions of the hole are less than the mean-free-path then we are
dealing with effusion through the hole, rather than hydrodynamical flow. In this case, the equilibrium
condition requires that the mass of gas on each side remain constant. In other words, the effusion rates in
both directions must be equal. Thus, it follows from Equation (7.241) that
--otherwise, the
pressure difference would give rise to bulk motion of the gas from one side of the container to the other,
until the pressures were equalized. But, if the dimensions of the hole are less than the mean-free-path then we are
dealing with effusion through the hole, rather than hydrodynamical flow. In this case, the equilibrium
condition requires that the mass of gas on each side remain constant. In other words, the effusion rates in
both directions must be equal. Thus, it follows from Equation (7.241) that