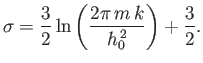Next: Gibb's Paradox
Up: Applications of Statistical Thermodynamics
Previous: Partition Function
Ideal Monatomic Gas
Let us now practice calculating thermodynamic relations using the partition
function by considering an example with which we are already quite familiar:
namely,
an ideal monatomic gas. Consider a gas consisting of  identical monatomic
molecules of mass
identical monatomic
molecules of mass  , enclosed in a container of volume
, enclosed in a container of volume  .
Let us denote the position and momentum
vectors of the
.
Let us denote the position and momentum
vectors of the  th molecule by
th molecule by 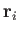 and
and
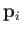 , respectively.
Because the gas is ideal, there are no interatomic forces, and the
total energy
is simply the sum of the individual kinetic energies of the molecules:
, respectively.
Because the gas is ideal, there are no interatomic forces, and the
total energy
is simply the sum of the individual kinetic energies of the molecules:
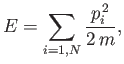 |
(7.63) |
where
 .
.
Let us treat the problem classically. In this approach, we divide up phase-space
into cells of equal volume  . Here,
. Here, 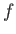 is the number of degrees of
freedom, and
is the number of degrees of
freedom, and  is a small constant with dimensions of angular momentum that
parameterizes the precision to which the positions and momenta of molecules
are determined. (See Section 3.2.)
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
is a small constant with dimensions of angular momentum that
parameterizes the precision to which the positions and momenta of molecules
are determined. (See Section 3.2.)
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
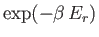 taken over all possible states, where
taken over all possible states, where 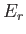 is the energy of state
is the energy of state  .
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
.
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
 |
(7.64) |
where 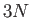 is the number of degrees of freedom of a monatomic gas containing
is the number of degrees of freedom of a monatomic gas containing
 molecules. Making use of Equation (7.63),
the previous
expression reduces to
molecules. Making use of Equation (7.63),
the previous
expression reduces to
 |
(7.65) |
Note that the integral over the coordinates of a given
molecule simply yields the volume
of the container,  , because the energy,
, because the energy,  , is independent of the
locations of the molecules
in an ideal gas. There are
, is independent of the
locations of the molecules
in an ideal gas. There are  such integrals, so we obtain the factor
such integrals, so we obtain the factor
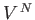 in the previous expression. Note, also, that
each of the integrals over the molecular momenta in Equation (7.65)
are identical: they differ only by irrelevant dummy variables of integration.
It follows that the partition function
in the previous expression. Note, also, that
each of the integrals over the molecular momenta in Equation (7.65)
are identical: they differ only by irrelevant dummy variables of integration.
It follows that the partition function 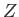 of the gas is made up of the product of
of the gas is made up of the product of
 identical factors: that is,
identical factors: that is,
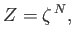 |
(7.66) |
where
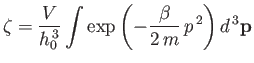 |
(7.67) |
is the partition function for a single molecule. Of course, this
result is obvious, because we have already shown that the partition function for
a system made up of a number of weakly interacting subsystems is just the
product of the partition functions of the subsystems. (See Section 7.6.)
The integral in Equation (7.67) is easily evaluated:
where use has been made of Equation (2.79). Thus,
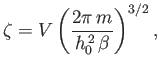 |
(7.69) |
and
![$\displaystyle \ln Z = N\ln \zeta = N \left[\ln V - \frac{3}{2}\ln \beta +\frac{3}{2} \ln\left(\frac{2\pi m}{h_0^{ 2}}\right)\right].$](img1398.png) |
(7.70) |
The expression for the mean pressure, (7.50), yields
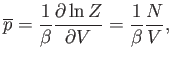 |
(7.71) |
which reduces to the ideal gas equation of state
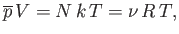 |
(7.72) |
where use has been made of
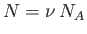 and
and
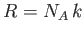 . According to Equation (7.35), the mean
energy of the gas is given by
. According to Equation (7.35), the mean
energy of the gas is given by
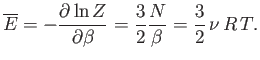 |
(7.73) |
Note that the internal
energy is a function of temperature alone, with no dependence on
volume. The molar heat capacity at constant volume of the gas is given by
 |
(7.74) |
so the mean energy can be written
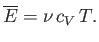 |
(7.75) |
We have seen all of the previous results
before. Let us
now use the partition function to calculate a new result. The entropy of the
gas can be calculated quite simply from the expression
 |
(7.76) |
Thus,
![$\displaystyle S = \nu R \left[ \ln V -\frac{3}{2} \ln \beta + \frac{3}{2}\ln \left(\frac{2\pi m }{h_0^{ 2}}\right) + \frac{3}{2} \right],$](img1406.png) |
(7.77) |
or
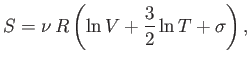 |
(7.78) |
where
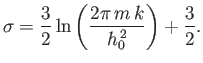 |
(7.79) |
The previous expression for the entropy of an ideal gas is certainly a new result.
Unfortunately, it is also quite obviously incorrect.



Next: Gibb's Paradox
Up: Applications of Statistical Thermodynamics
Previous: Partition Function
Richard Fitzpatrick
2016-01-25
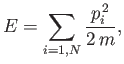
![]() . Here,
. Here, ![]() is the number of degrees of
freedom, and
is the number of degrees of
freedom, and ![]() is a small constant with dimensions of angular momentum that
parameterizes the precision to which the positions and momenta of molecules
are determined. (See Section 3.2.)
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
is a small constant with dimensions of angular momentum that
parameterizes the precision to which the positions and momenta of molecules
are determined. (See Section 3.2.)
Each cell in phase-space corresponds to a different state.
The partition function is the sum of the Boltzmann factor
![]() taken over all possible states, where
taken over all possible states, where ![]() is the energy of state
is the energy of state ![]() .
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,
.
Classically, we can approximate the summation over cells in phase-space
as an integration over all phase-space. Thus,



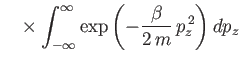
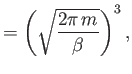
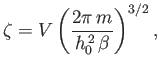
![$\displaystyle \ln Z = N\ln \zeta = N \left[\ln V - \frac{3}{2}\ln \beta +\frac{3}{2} \ln\left(\frac{2\pi m}{h_0^{ 2}}\right)\right].$](img1398.png)
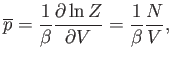
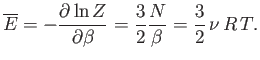

![$\displaystyle S = \nu R \left[ \ln V -\frac{3}{2} \ln \beta + \frac{3}{2}\ln \left(\frac{2\pi m }{h_0^{ 2}}\right) + \frac{3}{2} \right],$](img1406.png)