


Next: Van der Waals Gas
Up: Classical Thermodynamics
Previous: General Relation Between Specific
Consider a rigid container that is thermally insulated. The container is divided into two
compartments separated by a valve that is initially closed. One compartment, of volume 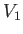 ,
contains the gas under investigation. The other compartment is empty. The initial temperature of the
system is
,
contains the gas under investigation. The other compartment is empty. The initial temperature of the
system is  . The valve is now opened, and the gas is free to expand so as to fill the entire
container, whose volume is
. The valve is now opened, and the gas is free to expand so as to fill the entire
container, whose volume is 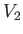 . What is the temperature,
. What is the temperature, 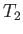 , of the gas after the final
equilibrium state has been reached?
, of the gas after the final
equilibrium state has been reached?
Because the system consisting of the gas and the container is adiabatically insulated, no heat flows
into the system: that is,
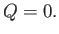 |
(6.144) |
Furthermore, the system does no work in the expansion process: that is,
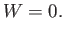 |
(6.145) |
It follows from the first law of thermodynamics that the total energy of the system is
conserved: that is,
 |
(6.146) |
Let us assume that the container itself has negligible heat capacity (which, it turns out, is not a particularly realistic assumption--see later), so that the internal energy of the container does not
change. Under these circumstances, the energy change of the system is equivalent to that of the gas.
The conservation of energy, (6.146), thus reduces to
 |
(6.147) |
where 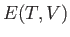 is the gas's internal energy.
is the gas's internal energy.
To predict the outcome of the experiment, it is only necessary to know the internal energy of the gas,
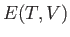 , as a function of the temperature and the volume. If the initial parameters,
, as a function of the temperature and the volume. If the initial parameters,  and
and
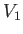 , are known, as well as the final volume,
, are known, as well as the final volume, 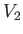 , then Equation (6.147) yields
an equation that specifies the unknown final temperature,
, then Equation (6.147) yields
an equation that specifies the unknown final temperature, 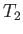 .
.
For an ideal gas, the internal energy is independent of the volume: that is, 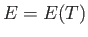 . (See Section 6.2.)
In this case, Equation (6.147) yields
. (See Section 6.2.)
In this case, Equation (6.147) yields
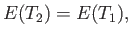 |
(6.148) |
which implies that 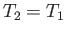 . In other words, there is no temperature change in the free expansion
of an ideal gas.
. In other words, there is no temperature change in the free expansion
of an ideal gas.
The change in temperature of an non-ideal gas that undergoes free expansion can be written
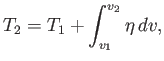 |
(6.149) |
where
 |
(6.150) |
is termed the Joule coefficient. Here, 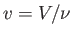 is the molar volume, where
is the molar volume, where 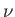 is the number of moles
of gas in the container. Furthermore,
is the number of moles
of gas in the container. Furthermore,
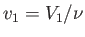 and
and
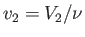 .
.
According to the first law of thermodynamics,
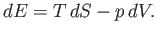 |
(6.151) |
However, if the internal energy is constant then we can write
![$\displaystyle 0=T\left[\left(\frac{\partial S}{\partial T}\right)_VdT + \left(\frac{\partial S}{\partial V}\right)_TdV\right]-p dV.$](img1093.png) |
(6.152) |
With the aid of Equations (6.109) and (6.120), this becomes
![$\displaystyle 0=C_V dT + \left[T\left(\frac{\partial p}{\partial T}\right)_V -p\right]dV.$](img1094.png) |
(6.153) |
Hence,
![$\displaystyle \left(\frac{\partial T}{\partial V}\right)_E =-\left.\left[T\left(\frac{\partial p}{\partial T}\right)_V -p\right]\right/C_V,$](img1095.png) |
(6.154) |
and the Joule coefficient can be written
![$\displaystyle \eta = -\left.\left[T\left(\frac{\partial p}{\partial T}\right)_V...
...ight]\right/c_V = -\left.\left(\frac{T \alpha_V}{\kappa_T}-p\right)\right/c_V.$](img1096.png) |
(6.155) |
[See Equation (6.132).]
Note that all terms on the right-hand side of the previous expression are easily measurable.



Next: Van der Waals Gas
Up: Classical Thermodynamics
Previous: General Relation Between Specific
Richard Fitzpatrick
2016-01-25
![]() , as a function of the temperature and the volume. If the initial parameters,
, as a function of the temperature and the volume. If the initial parameters, ![]() and
and
![]() , are known, as well as the final volume,
, are known, as well as the final volume, ![]() , then Equation (6.147) yields
an equation that specifies the unknown final temperature,
, then Equation (6.147) yields
an equation that specifies the unknown final temperature, ![]() .
.
![]() . (See Section 6.2.)
In this case, Equation (6.147) yields
. (See Section 6.2.)
In this case, Equation (6.147) yields

![$\displaystyle 0=T\left[\left(\frac{\partial S}{\partial T}\right)_VdT + \left(\frac{\partial S}{\partial V}\right)_TdV\right]-p dV.$](img1093.png)
![$\displaystyle 0=C_V dT + \left[T\left(\frac{\partial p}{\partial T}\right)_V -p\right]dV.$](img1094.png)
![$\displaystyle \left(\frac{\partial T}{\partial V}\right)_E =-\left.\left[T\left(\frac{\partial p}{\partial T}\right)_V -p\right]\right/C_V,$](img1095.png)