 |
(6.68) |
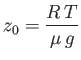 |
(6.69) |
We have discovered that, in an isothermal atmosphere, the pressure
decreases exponentially with increasing height.
Because the temperature is assumed to be constant, and
![]() [see Equation (6.66)],
it follows that the density also decreases exponentially with the same scale-height
as the pressure.
According to Equation (6.68), the
pressure, or the density, of the atmosphere
decreases by a factor 10 every
[see Equation (6.66)],
it follows that the density also decreases exponentially with the same scale-height
as the pressure.
According to Equation (6.68), the
pressure, or the density, of the atmosphere
decreases by a factor 10 every
![]() , or 19.3 kilometers,
increase in altitude above sea level. Clearly, the effective height of the atmosphere is
very small compared to the Earth's radius, which is about
, or 19.3 kilometers,
increase in altitude above sea level. Clearly, the effective height of the atmosphere is
very small compared to the Earth's radius, which is about ![]() kilometers.
In other words, the atmosphere constitutes a relatively thin layer covering
the surface of the Earth.
Incidentally, this justifies our neglect of the decrease of
kilometers.
In other words, the atmosphere constitutes a relatively thin layer covering
the surface of the Earth.
Incidentally, this justifies our neglect of the decrease of ![]() with increasing
altitude.
with increasing
altitude.
One of the highest points in the United States of America is
the peak of Mount Elbert in Colorado.
This peak lies ![]() feet, or about
feet, or about ![]() kilometers, above sea level. At this altitude, Equation (6.68) predicts that the air pressure should be about
kilometers, above sea level. At this altitude, Equation (6.68) predicts that the air pressure should be about ![]() atmospheres.
Surprisingly enough, after a few days
acclimatization, people can survive quite comfortably at this sort of
pressure.
In the highest inhabited regions of the Andes and Tibet, the air pressure
falls to about
atmospheres.
Surprisingly enough, after a few days
acclimatization, people can survive quite comfortably at this sort of
pressure.
In the highest inhabited regions of the Andes and Tibet, the air pressure
falls to about ![]() atmospheres. Humans can just about survive at such
pressures. However, people cannot survive for any extended period in air pressures
below half an atmosphere. This sets an upper limit on the altitude of permanent
human habitation, which is about
atmospheres. Humans can just about survive at such
pressures. However, people cannot survive for any extended period in air pressures
below half an atmosphere. This sets an upper limit on the altitude of permanent
human habitation, which is about ![]() feet, or
feet, or ![]() kilometers, above
sea level. Incidentally, this is also the maximum altitude at which a pilot
can fly an unpressurized
aircraft without requiring additional oxygen.
kilometers, above
sea level. Incidentally, this is also the maximum altitude at which a pilot
can fly an unpressurized
aircraft without requiring additional oxygen.
The highest point in the world is, of course, the peak of
Mount Everest in Nepal. This peak lies at
an altitude of ![]() feet, or
feet, or ![]() kilometers, above sea level,
where we expect the air pressure to
be a mere
kilometers, above sea level,
where we expect the air pressure to
be a mere ![]() atmospheres. This explains why Mount Everest was only conquered
after lightweight portable oxygen cylinders were invented. Admittedly,
some climbers have subsequently ascended Mount Everest without the aid of
additional oxygen,
but this is a very foolhardy venture, because,
above
atmospheres. This explains why Mount Everest was only conquered
after lightweight portable oxygen cylinders were invented. Admittedly,
some climbers have subsequently ascended Mount Everest without the aid of
additional oxygen,
but this is a very foolhardy venture, because,
above ![]() feet, the climbers are slowly dying.
feet, the climbers are slowly dying.
Commercial airliners fly at a cruising altitude of ![]() feet. At
this altitude, we expect the air pressure to be only
feet. At
this altitude, we expect the air pressure to be only ![]() atmospheres,
which explains
why airline cabins are pressurized. In fact, the cabins are only pressurized to
atmospheres,
which explains
why airline cabins are pressurized. In fact, the cabins are only pressurized to
![]() atmospheres (which accounts for the ``popping'' of passangers
ears during
air travel). The reason for this partial pressurization is quite simple. At
atmospheres (which accounts for the ``popping'' of passangers
ears during
air travel). The reason for this partial pressurization is quite simple. At
![]() feet, the pressure difference between the air in the cabin, and hence that
outside, is
about half an atmosphere. Clearly, the walls of the cabin must be strong enough
to support this pressure difference, which means that they must be of a
certain thickness, and, hence, that the aircraft must be of a certain weight. If
the cabin were fully pressurized then the pressure difference at cruising altitude
would increase by about 30%, which means that the cabin walls would
have to be much thicker, and, hence, the aircraft would have to be
substantially heavier. So, a fully pressurized
aircraft would be more comfortable to fly in (because your ears would not ``pop''),
but it would also be far less economical to operate.
feet, the pressure difference between the air in the cabin, and hence that
outside, is
about half an atmosphere. Clearly, the walls of the cabin must be strong enough
to support this pressure difference, which means that they must be of a
certain thickness, and, hence, that the aircraft must be of a certain weight. If
the cabin were fully pressurized then the pressure difference at cruising altitude
would increase by about 30%, which means that the cabin walls would
have to be much thicker, and, hence, the aircraft would have to be
substantially heavier. So, a fully pressurized
aircraft would be more comfortable to fly in (because your ears would not ``pop''),
but it would also be far less economical to operate.