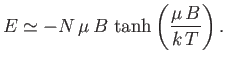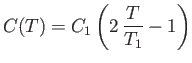Next: Classical Thermodynamics
Up: Statistical Thermodynamics
Previous: Laws of Thermodynamics
- A box is separated by a partition that divides its volume in the ratio
3:1. The larger portion of the box contains 1000 molecules of Ne gas, and the smaller,
100 molecules of He gas. A small hole is punctured in the partition, and the
system is allowed to settle down and attain an equilibrium state.
- Find the mean number of molecules of each type on either side of the partition.
- What is the probability of finding 1000 molecules of Ne gas in the larger
partition, and 100 molecules of He gas in the smaller (in other words, the same distribution
as in the initial system)?
- Consider an isolated system consisting of a large number,
 , of very weakly-interacting localized particles of spin
, of very weakly-interacting localized particles of spin  . Each particle has a magnetic moment,
. Each particle has a magnetic moment,
 , that can point either parallel or antiparallel to an applied magnetic
field,
, that can point either parallel or antiparallel to an applied magnetic
field,  . The energy,
. The energy,  , of the system is then
, of the system is then
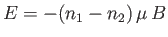 , where
, where
 is the number of spins aligned parallel to
is the number of spins aligned parallel to  , and
, and 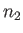 the number
of antiparallel spins.
the number
of antiparallel spins.
- Consider the energy range between
 and
and
 , where
, where 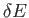 is very
small compared to
is very
small compared to  , but is microscopically large, so that
, but is microscopically large, so that
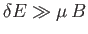 .
Show that the total number of states lying in this energy range is
.
Show that the total number of states lying in this energy range is
- Write down an expression for
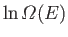 . Simplify this expression
using Stirling's approximation (i.e.
. Simplify this expression
using Stirling's approximation (i.e.
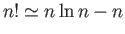 ) to obtain
) to obtain
- Use the definition
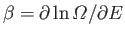 (where
(where
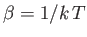 ) to show that the energy of the system can be written
) to show that the energy of the system can be written
- Under what circumstances is the temperature negative?
- Suppose that two otherwise identical spin systems with equal and opposite
temperatures are brought into thermal contact. What is the final temperature of
the overall system?
- A glass bulb contains air at room temperature and at a pressure of 1 atmosphere.
It is placed in a far larger
chamber filled with helium gas at 1 atmosphere and at room
temperature. A few months later, the experimenter happens to read in a journal that
the particular glass of which the bulb is made is quite permeable to helium,
but not to any other gas. Assuming that equilibrium has been reached by this time,
what gas pressure will the experimenter measure inside the bulb when he/she goes
back to check?
- The heat absorbed by a mole of ideal gas in a quasi-static process in
which the temperature,
 , changes by
, changes by 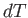 , and the volume,
, and the volume,  , by
, by  , is
given by
, is
given by
where  is its constant molar specific heat at constant volume, and
is its constant molar specific heat at constant volume, and 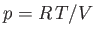 is
its pressure. Find an expression for the change in entropy of
the gas in a quasi-static process which takes it from the initial values
of temperature and volume
is
its pressure. Find an expression for the change in entropy of
the gas in a quasi-static process which takes it from the initial values
of temperature and volume 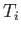 and
and 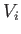 , respectively, to the final values
, respectively, to the final values  and
and 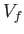 , respectively.
Does the answer depend on the process involved in going from the initial
to the final state? What is the relationship between the temperature and
the volume in an adiabatic process (i.e. a quasi-static process in which
no heat is absorbed)? What is the change in entropy in an adiabatic
process in which the volume changes from an initial value
, respectively.
Does the answer depend on the process involved in going from the initial
to the final state? What is the relationship between the temperature and
the volume in an adiabatic process (i.e. a quasi-static process in which
no heat is absorbed)? What is the change in entropy in an adiabatic
process in which the volume changes from an initial value 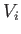 to
a final value
to
a final value 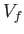 ?
?
- A solid contains
 magnetic atoms having spin
magnetic atoms having spin 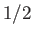 . At sufficiently
high temperatures, each spin is completely randomly oriented. In other words, it is equally
likely to be in either one of two possible states. But at sufficiently low
temperature, the interactions between the magnetic atoms causes them to
exhibit ferromagnetism, with the result that their spins become oriented in
the same direction. A very crude approximation suggests that
the spin-dependent contribution,
. At sufficiently
high temperatures, each spin is completely randomly oriented. In other words, it is equally
likely to be in either one of two possible states. But at sufficiently low
temperature, the interactions between the magnetic atoms causes them to
exhibit ferromagnetism, with the result that their spins become oriented in
the same direction. A very crude approximation suggests that
the spin-dependent contribution, 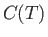 , to the heat capacity of the solid has an
approximate temperature dependence given by
, to the heat capacity of the solid has an
approximate temperature dependence given by
for
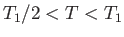 , and
, and
otherwise. The abrupt increase in specific heat as  is reduced below
is reduced below  is
due to the onset of ferromagnetic behavior.
Find two expressions for the increase in entropy as the temperature of
the system is raised from a value below
is
due to the onset of ferromagnetic behavior.
Find two expressions for the increase in entropy as the temperature of
the system is raised from a value below 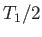 to one above
to one above  . By
equating these two expressions, show that
. By
equating these two expressions, show that



Next: Classical Thermodynamics
Up: Statistical Thermodynamics
Previous: Laws of Thermodynamics
Richard Fitzpatrick
2016-01-25
 and
and
 , where
, where 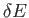 is very
small compared to
is very
small compared to  , but is microscopically large, so that
, but is microscopically large, so that
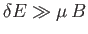 .
Show that the total number of states lying in this energy range is
.
Show that the total number of states lying in this energy range is
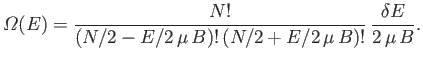
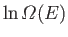 . Simplify this expression
using Stirling's approximation (i.e.
. Simplify this expression
using Stirling's approximation (i.e.
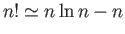 ) to obtain
) to obtain
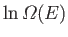
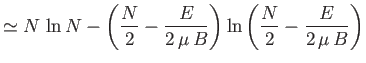
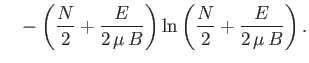
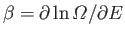 (where
(where
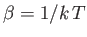 ) to show that the energy of the system can be written
) to show that the energy of the system can be written