The modern interpretation of heat is, or course, somewhat different to Lavoisier's
calorific theory. Nevertheless, there is an important subset
of problems, involving heat flow, for which Lavoisier's approach is
rather useful.
These problems often crop up as examination questions.
For example: ``A clean dry copper
calorimeter contains 100 grams of water at 30![]() degrees centigrade.
A 10 gram block of copper heated to 60
degrees centigrade.
A 10 gram block of copper heated to 60![]() centigrade is added. What is the final
temperature of the mixture?''.
How do we approach this type of problem? According to Lavoisier's theory, there is an
analogy between heat flow and incompressible
fluid flow under gravity.
The same volume of liquid added to
containers of different (uniform) cross-sectional area fills them to different heights.
If the volume is
centigrade is added. What is the final
temperature of the mixture?''.
How do we approach this type of problem? According to Lavoisier's theory, there is an
analogy between heat flow and incompressible
fluid flow under gravity.
The same volume of liquid added to
containers of different (uniform) cross-sectional area fills them to different heights.
If the volume is ![]() , and the cross-sectional area is
, and the cross-sectional area is ![]() , then the height is
, then the height is
![]() . In a similar manner, the same quantity of heat added to different bodies
causes them to rise to different temperatures. If
. In a similar manner, the same quantity of heat added to different bodies
causes them to rise to different temperatures. If ![]() is the heat and
is the heat and
![]() is the (absolute) temperature then
is the (absolute) temperature then
![]() , where the constant
, where the constant ![]() is termed the heat capacity.
[This is a somewhat oversimplified example. In general, the heat capacity is
a function of temperature, so that
is termed the heat capacity.
[This is a somewhat oversimplified example. In general, the heat capacity is
a function of temperature, so that
![]() .]
If two containers, filled to different heights,
with a free-flowing incompressible fluid
are connected together at the bottom, via a small pipe,
then fluid will flow under gravity,
from one
to the other, until the two heights are the same. The final height is easily
calculated by equating the total fluid volume in the initial and final
states. Thus,
.]
If two containers, filled to different heights,
with a free-flowing incompressible fluid
are connected together at the bottom, via a small pipe,
then fluid will flow under gravity,
from one
to the other, until the two heights are the same. The final height is easily
calculated by equating the total fluid volume in the initial and final
states. Thus,
| (4.1) |
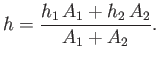 |
(4.2) |
| (4.3) |
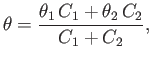 |
(4.4) |
The analogy between heat flow and fluid flow works because, in Lavoisier's theory, heat is a conserved quantity, just like the volume of an incompressible fluid. In fact, Lavoisier postulated that heat was an element. Note that atoms were thought to be indestructible before nuclear reactions were discovered, so the total amount of each element in the cosmos was assumed to be a constant. Thus, if Lavoisier had cared to formulate a law of thermodynamics from his calorific theory then he would have said that the total amount of heat in the universe was a constant.
In 1798, Benjamin Thompson, an Englishman who spent his early years in
pre-revolutionary
America, was minister for war and police in the German state of Bavaria.
One of his jobs was to oversee the boring of cannons in the state arsenal.
Thompson was struck by the
enormous, and seemingly inexhaustible, amount of heat generated in this process.
He simply could not understand where all this
heat was coming from. According to Lavoisier's calorific theory, the heat
must flow into the cannon from its immediate surroundings, which should, therefore,
become colder.
The flow should also eventually cease when all of the available heat has been
extracted.
In fact, Thompson observed that the surroundings of the cannon
got hotter, not colder,
and that the heating process continued unabated as long as the
boring machine was operating. Thompson postulated that some of the mechanical
work done
on the cannon by the boring machine was being converted into heat. At the time,
this was quite a revolutionary concept, and most people were not ready to accept it.
This is somewhat surprising, because, by the end of the eighteenth century,
the conversion of heat into
work, by steam engines, was quite commonplace.
Nevertheless, the conversion of work into heat did not gain broad acceptance until
1849, when an English physicist called
James Prescott Joule published the results of a long and
painstaking series of experiments. Joule confirmed that work could indeed
be converted
into heat. Moreover, he found that the same amount of work always generates
the same quantity of
heat. This is
true regardless of the nature of the work (e.g., mechanical, electrical,
et cetera). Joule was able to formulate what became known as
the work equivalent of heat.
Namely, that 1 newton meter of work is equivalent to ![]() calories of heat.
A calorie is the amount of heat required to raise the temperature of 1 gram of
water by 1 degree centigrade. Nowadays, we measure both heat and work using the
same units, so that one newton meter, or joule, of work is equivalent to
one joule of heat.
calories of heat.
A calorie is the amount of heat required to raise the temperature of 1 gram of
water by 1 degree centigrade. Nowadays, we measure both heat and work using the
same units, so that one newton meter, or joule, of work is equivalent to
one joule of heat.
In 1850, the German physicist Clausius correctly postulated that the essential conserved quantity is neither heat nor work, but some combination of the two which quickly became known as energy, from the Greek energeia meaning ``activity" or ``action.'' According to Clausius, the change in the internal energy of a macroscopic body can be written
| (4.5) |