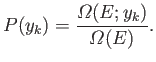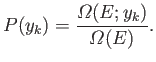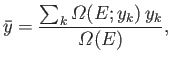Next: Behavior of Density of
Up: Statistical Mechanics
Previous: Reversibility and Irreversibility
The principle of equal a priori probabilities is fundamental to all of
statistical mechanics, and allows a complete description of the properties
of macroscopic systems in equilibrium. In principle,
statistical mechanics calculations are
very simple. Consider a system in equilibrium that is isolated, so that its
total energy is known to have a constant value lying somewhere in the range  to
to
 . In order to make statistical predictions, we focus attention
on an ensemble of such systems, all of which have their energy in this range.
Let
. In order to make statistical predictions, we focus attention
on an ensemble of such systems, all of which have their energy in this range.
Let
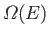 be the total number of different states in the ensemble with
energies in the specified range. Suppose that, among these states, there are
a number
be the total number of different states in the ensemble with
energies in the specified range. Suppose that, among these states, there are
a number
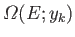 for which some parameter,
for which some parameter,  , of the system
assumes the discrete value
, of the system
assumes the discrete value 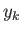 . (This discussion can easily
be generalized to deal with a parameter that can assume a continuous range of
values.) The principle of equal a priori probabilities tells us
that all of the
. (This discussion can easily
be generalized to deal with a parameter that can assume a continuous range of
values.) The principle of equal a priori probabilities tells us
that all of the
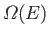 accessible states of the system are equally likely
to occur in the ensemble. It follows that the probability,
accessible states of the system are equally likely
to occur in the ensemble. It follows that the probability, 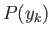 , that the
parameter
, that the
parameter  of the system assumes the value
of the system assumes the value 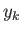 is simply
is simply
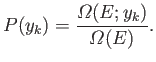 |
(3.18) |
Clearly, the mean value of  for the system is given by
for the system is given by
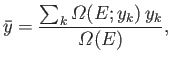 |
(3.19) |
where the sum is over all possible values that  can assume.
In the previous formula, it is tacitly assumed that
can assume.
In the previous formula, it is tacitly assumed that
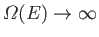 ,
which is generally the case in thermodynamic systems.
,
which is generally the case in thermodynamic systems.
It can be seen that, using the principle of equal a priori
probabilities, all calculations in statistical mechanics
reduce to counting states, subject to
various constraints. In principle, this is a fairly straightforward task.
In practice, problems arise if
the constraints become too complicated. These problems can usually be
overcome with a little mathematical ingenuity.
Nevertheless, there is no doubt that this
type of calculation is far easier than trying to solve the classical equations
of motion
(or Schrödinger's equation) directly for a many-particle system.



Next: Behavior of Density of
Up: Statistical Mechanics
Previous: Reversibility and Irreversibility
Richard Fitzpatrick
2016-01-25