


Next: Statistical Mechanics
Up: Probability Theory
Previous: Central Limit Theorem
- Let
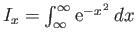 and
and
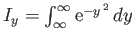 .
Show that
.
Show that
where
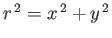 . Hence, deduce that
. Hence, deduce that
 .
.
- Show that
Hence, deduce that
- Confirm that
where
- Show that the probability of throwing 6 points or less with three (six-sided) dice is
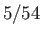 .
.
- Consider a game in which six (six-sided) dice are rolled. Find the probability
of obtaining:
- exactly one ace.
- at least one ace.
- exactly two aces.
- In the game of Russian roulette, one inserts a single cartridge into the drum
of a revolver, leaving the other five chambers of the drum empty. One then spins
the drum, aims at one's head, and pulls the trigger.
- Show that the probability of still being alive after playing the game
 times is
times is
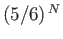 .
.
- Show that the probability of surviving
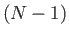 turns in this game, and then being
shot the
turns in this game, and then being
shot the  th times one pulls the trigger, is
th times one pulls the trigger, is
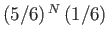 .
.
- Show that the mean number of times a player gets to pull the trigger is
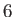 .
.
- A battery of total emf
 is connected to a resistor
is connected to a resistor 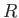 . As a result, an
amount of power
. As a result, an
amount of power
 is dissipated in the resistor. The battery itself
consists of
is dissipated in the resistor. The battery itself
consists of  individual cells connected in series, so that
individual cells connected in series, so that  is equal
to the sum of the emf's of all these cells. The battery is old, however, so that
not all cells are in perfect condition. Thus, there is a probability
is equal
to the sum of the emf's of all these cells. The battery is old, however, so that
not all cells are in perfect condition. Thus, there is a probability  that the
emf of any individual cell has its normal value
that the
emf of any individual cell has its normal value  ; and a probability
; and a probability 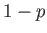 that the emf of any individual cell is zero because the cell has become internally
shorted. The individual cells are statistically independent of each other.
Under these conditions, show that the mean power,
that the emf of any individual cell is zero because the cell has become internally
shorted. The individual cells are statistically independent of each other.
Under these conditions, show that the mean power,
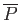 , dissipated in the
resistor, is
, dissipated in the
resistor, is
- A drunk starts out from a lamppost in the middle of a street, taking steps
of uniform length
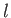 to the right or to the left with equal probability.
to the right or to the left with equal probability.
- Show that the average distance from the lamppost after
 steps is zero.
steps is zero.
- Show that the root-mean-square distance (i.e. the square-root of the
mean of the distance squared) from the lamppost after
 steps is
steps is
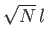 .
.
- Show that the probability that the drunk will return to the lamppost after
 steps is zero if
steps is zero if  is odd, and
is odd, and
if  is even.
is even.
- A molecule in a gas moves equal distances
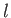 between collisions with equal
probabilities in any direction. Show that, after a total of
between collisions with equal
probabilities in any direction. Show that, after a total of  such displacements,
the mean-square displacement,
such displacements,
the mean-square displacement,
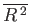 , of the molecule from its starting
point is
, of the molecule from its starting
point is
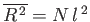 .
.
- A penny is tossed 400 times. Find the probability of getting 215 heads.
(Use the Gaussian distribution.)
- Suppose that the probability density for the speed
 of a car on a highway
is given by
of a car on a highway
is given by
where
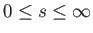 . Here,
. Here,  and
and 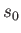 are positive constants. More
explicitly,
are positive constants. More
explicitly,
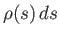 gives the probability that a car has a speed
between
gives the probability that a car has a speed
between  and
and 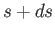 .
.
- Determine
 in terms of
in terms of 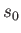 .
.
- What is the mean value of the speed?
- What is the ``most probable'' speed: that is, the speed
for which the probability density has a maximum.
- What is the probability that a car has a speed more than three times as large
as the mean value?



Next: Statistical Mechanics
Up: Probability Theory
Previous: Central Limit Theorem
Richard Fitzpatrick
2016-01-25
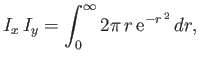
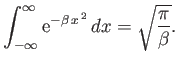
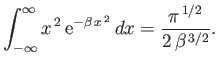



![$\displaystyle {\cal P}(n)=\frac{1}{\sqrt{2\pi} {\mit\Delta}^\ast n}\exp\left[-\frac{(n-\bar{n})^{ 2}}{2 ({\mit\Delta}^\ast n)^{ 2}}\right].
$](img279.png)
 times is
times is
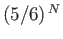 .
.
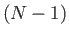 turns in this game, and then being
shot the
turns in this game, and then being
shot the  th times one pulls the trigger, is
th times one pulls the trigger, is
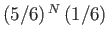 .
.
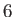 .
.
![$\displaystyle \overline{P}= \frac{p^{ 2} V^{ 2}}{R}\left[1-\frac{(1-p)}{N p}\right].
$](img289.png)
 steps is zero.
steps is zero.
 steps is
steps is
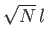 .
.
 steps is zero if
steps is zero if  is odd, and
is odd, and
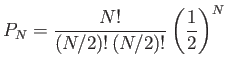
 is even.
is even.

 in terms of
in terms of 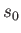 .
.