Next: Central Limit Theorem
Up: Probability Theory
Previous: Application to Binomial Probability
Gaussian Probability Distribution
Consider a very large number of observations, 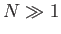 , made on a system
with two possible outcomes.
Suppose that the probability of outcome 1 is sufficiently large that
the average number of occurrences after
, made on a system
with two possible outcomes.
Suppose that the probability of outcome 1 is sufficiently large that
the average number of occurrences after  observations is much greater than unity: that is,
observations is much greater than unity: that is,
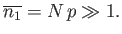 |
(2.54) |
In this limit, the standard deviation of  is also much greater than unity,
is also much greater than unity,
 |
(2.55) |
implying that there are very many probable values of  scattered about the
mean value,
scattered about the
mean value,
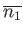 .
This suggests that the probability of obtaining
.
This suggests that the probability of obtaining  occurrences
of outcome 1
does not change significantly in going from one possible value of
occurrences
of outcome 1
does not change significantly in going from one possible value of
 to an adjacent value. In other words,
to an adjacent value. In other words,
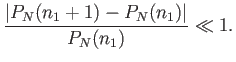 |
(2.56) |
In this situation, it is useful to regard the probability as a smooth
function of  . Let
. Let  be a continuous variable that is
interpreted as the number of occurrences of outcome 1 (after
be a continuous variable that is
interpreted as the number of occurrences of outcome 1 (after  observations) whenever it takes
on a positive integer value. The probability that
observations) whenever it takes
on a positive integer value. The probability that  lies between
lies between
 and
and 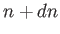 is defined
is defined
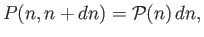 |
(2.57) |
where
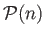 is called the probability density, and is independent
of
is called the probability density, and is independent
of  . The probability can be written in this form because
. The probability can be written in this form because
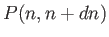 can always be expanded as a Taylor series in
can always be expanded as a Taylor series in  , and must go
to zero as
, and must go
to zero as
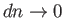 .
We can write
.
We can write
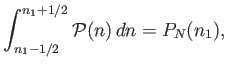 |
(2.58) |
which is equivalent to smearing out the discrete probability 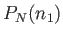 over the range
over the range
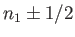 . Given Equations (2.38) and (2.56), the previous relation
can be approximated as
. Given Equations (2.38) and (2.56), the previous relation
can be approximated as
 |
(2.59) |
For large  , the relative width of the probability distribution function
is small: that is,
, the relative width of the probability distribution function
is small: that is,
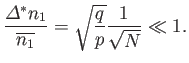 |
(2.60) |
This suggests that
 is strongly peaked around the mean value,
is strongly peaked around the mean value,
 . Suppose that
. Suppose that
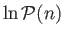 attains
its maximum value at
attains
its maximum value at
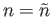 (where we expect
(where we expect
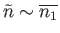 ). Let us Taylor expand
). Let us Taylor expand
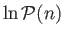 around
around
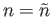 .
Note that we are expanding the slowly-varying function
.
Note that we are expanding the slowly-varying function
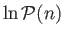 ,
rather than the rapidly-varying function
,
rather than the rapidly-varying function
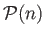 ,
because the Taylor expansion of
,
because the Taylor expansion of
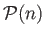 does not converge sufficiently rapidly in the
vicinity of
does not converge sufficiently rapidly in the
vicinity of
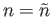 to be useful.
We can write
to be useful.
We can write
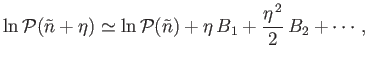 |
(2.61) |
where
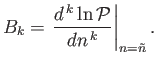 |
(2.62) |
By definition,
if
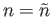 corresponds to the maximum
value of
corresponds to the maximum
value of
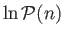 .
.
It follows from Equation (2.59) that
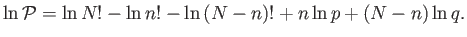 |
(2.65) |
If  is a large integer, such that
is a large integer, such that 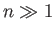 , then
, then  is almost a
continuous function of
is almost a
continuous function of  , because
, because  changes by only a relatively
small amount when
changes by only a relatively
small amount when  is incremented by unity.
Hence,
is incremented by unity.
Hence,
![$\displaystyle \frac{d\ln n!}{dn} \simeq \frac{\ln (n+1)!-\ln n!}{1} = \ln \left[\frac{(n+1)!}{n!}\right] = \ln (n+1),$](img236.png) |
(2.66) |
giving
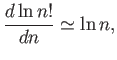 |
(2.67) |
for 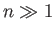 . The integral of this relation
. The integral of this relation
 |
(2.68) |
valid for 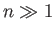 , is called Stirling's approximation, after the Scottish
mathematician James Stirling, who first obtained it in 1730.
, is called Stirling's approximation, after the Scottish
mathematician James Stirling, who first obtained it in 1730.
According to Equations (2.62), (2.65), and (2.67),
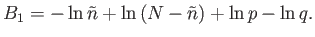 |
(2.69) |
Hence, if 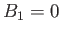 then
then
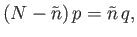 |
(2.70) |
giving
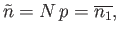 |
(2.71) |
because 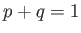 . [See Equations (2.11) and (2.43).] Thus, the maximum of
. [See Equations (2.11) and (2.43).] Thus, the maximum of
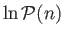 occurs exactly
at the mean value of
occurs exactly
at the mean value of  , which equals
, which equals
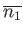 .
.
Further differentiation of Equation (2.69) yields [see Equation (2.62)]
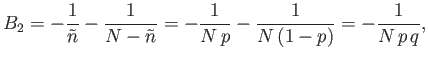 |
(2.72) |
because 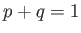 . Note that
. Note that 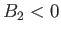 , as required. According to Equation (2.55), the previous relation
can also be written
, as required. According to Equation (2.55), the previous relation
can also be written
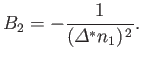 |
(2.73) |
It follows, from the previous analysis, that the Taylor expansion of
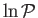 can be written
can be written
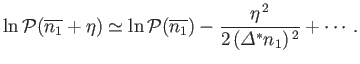 |
(2.74) |
Taking the exponential of both sides, we obtain
![$\displaystyle {\cal P}(n)\simeq {\cal P}(\overline{n_1})\exp\left[- \frac{(n-\overline{n_1})^{ 2}}{2 ({\mit\Delta}^\ast n_1)^{ 2}}\right].$](img248.png) |
(2.75) |
The constant
 is most conveniently
fixed by making use
of the normalization condition
is most conveniently
fixed by making use
of the normalization condition
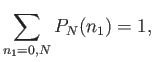 |
(2.76) |
which becomes
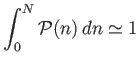 |
(2.77) |
for a continuous distribution function. Because we only expect
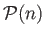 to be significant when
to be significant when
 lies in the relatively narrow range
lies in the relatively narrow range
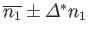 , the limits of integration in the previous
expression can be replaced by
, the limits of integration in the previous
expression can be replaced by
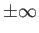 with negligible error.
Thus,
with negligible error.
Thus,
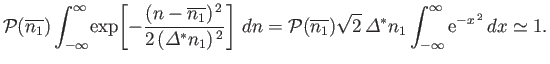 |
(2.78) |
As is well known,
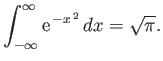 |
(2.79) |
(See Exercise 1.)
It follows from the normalization condition (2.78) that
 |
(2.80) |
Finally, we obtain
![$\displaystyle {\cal P}(n) \simeq \frac{1}{\sqrt{2\pi} {\mit\Delta}^\ast n_1}\...
...left[-\frac{(n-\overline{n_1})^{ 2}}{2 ({\mit\Delta}^\ast n_1)^{ 2}}\right].$](img257.png) |
(2.81) |
This is the famous Gaussian probability distribution, named after the
German mathematician Carl Friedrich Gauss, who discovered it while
investigating the distribution of errors in measurements. The Gaussian
distribution is only valid in the limits 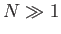 and
and
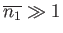 .
.
Suppose we were to
plot the probability 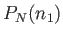 against the integer variable
against the integer variable  , and then
fit a continuous curve through the discrete points thus obtained. This curve
would be
equivalent to the continuous probability density curve
, and then
fit a continuous curve through the discrete points thus obtained. This curve
would be
equivalent to the continuous probability density curve
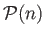 , where
, where
 is the continuous version of
is the continuous version of  . According to Equation (2.81), the
probability density attains its maximum
value when
. According to Equation (2.81), the
probability density attains its maximum
value when  equals the mean
of
equals the mean
of  , and
is also symmetric about this point. In fact, when plotted with the
appropriate ratio of vertical to horizontal scalings, the Gaussian probability
density curve looks rather like the outline of a
bell centered on
, and
is also symmetric about this point. In fact, when plotted with the
appropriate ratio of vertical to horizontal scalings, the Gaussian probability
density curve looks rather like the outline of a
bell centered on
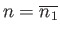 . Hence, this curve is sometimes
called a bell curve.
At one standard deviation away from the mean value--that is
. Hence, this curve is sometimes
called a bell curve.
At one standard deviation away from the mean value--that is
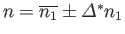 --the probability density is
about 61% of its peak value. At two standard deviations away from the mean
value, the probability density is about 13.5% of its peak value.
Finally,
at three standard deviations away from the mean value, the probability
density is only about 1% of its peak value. We conclude
that there is
very little chance that
--the probability density is
about 61% of its peak value. At two standard deviations away from the mean
value, the probability density is about 13.5% of its peak value.
Finally,
at three standard deviations away from the mean value, the probability
density is only about 1% of its peak value. We conclude
that there is
very little chance that  lies more than about three standard deviations
away from its mean value. In other words,
lies more than about three standard deviations
away from its mean value. In other words,  is almost certain to lie in the
relatively narrow range
is almost certain to lie in the
relatively narrow range
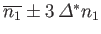 .
.
In the previous analysis, we went from a discrete probability
function, 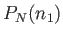 , to a continuous probability density,
, to a continuous probability density,
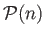 .
The normalization condition becomes
.
The normalization condition becomes
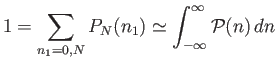 |
(2.82) |
under this transformation. Likewise, the evaluations of the mean and
variance of the distribution are written
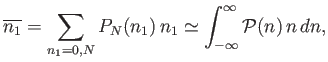 |
(2.83) |
and
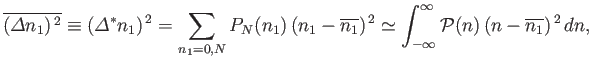 |
(2.84) |
respectively. These results
follow as simple generalizations of previously established results for
the discrete function 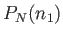 .
The limits of integration in the previous expressions
can be approximated as
.
The limits of integration in the previous expressions
can be approximated as
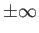 because
because
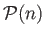 is only
non-negligible in a relatively narrow range of
is only
non-negligible in a relatively narrow range of  .
Finally, it is easily demonstrated that Equations (2.82)-(2.84) are indeed
true by substituting in the Gaussian probability density,
Equation (2.81), and then performing a few elementary integrals. (See Exercise 3.)
.
Finally, it is easily demonstrated that Equations (2.82)-(2.84) are indeed
true by substituting in the Gaussian probability density,
Equation (2.81), and then performing a few elementary integrals. (See Exercise 3.)



Next: Central Limit Theorem
Up: Probability Theory
Previous: Application to Binomial Probability
Richard Fitzpatrick
2016-01-25
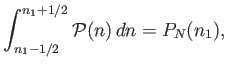
![]() , the relative width of the probability distribution function
is small: that is,
, the relative width of the probability distribution function
is small: that is,
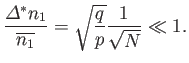
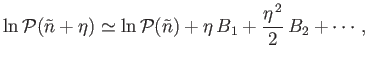
![$\displaystyle \frac{d\ln n!}{dn} \simeq \frac{\ln (n+1)!-\ln n!}{1} = \ln \left[\frac{(n+1)!}{n!}\right] = \ln (n+1),$](img236.png)
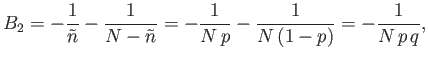
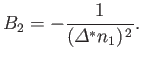
![]() can be written
can be written
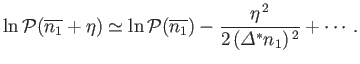
![$\displaystyle {\cal P}(n)\simeq {\cal P}(\overline{n_1})\exp\left[- \frac{(n-\overline{n_1})^{ 2}}{2 ({\mit\Delta}^\ast n_1)^{ 2}}\right].$](img248.png)
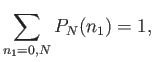
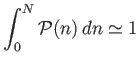

![]() against the integer variable
against the integer variable ![]() , and then
fit a continuous curve through the discrete points thus obtained. This curve
would be
equivalent to the continuous probability density curve
, and then
fit a continuous curve through the discrete points thus obtained. This curve
would be
equivalent to the continuous probability density curve
![]() , where
, where
![]() is the continuous version of
is the continuous version of ![]() . According to Equation (2.81), the
probability density attains its maximum
value when
. According to Equation (2.81), the
probability density attains its maximum
value when ![]() equals the mean
of
equals the mean
of ![]() , and
is also symmetric about this point. In fact, when plotted with the
appropriate ratio of vertical to horizontal scalings, the Gaussian probability
density curve looks rather like the outline of a
bell centered on
, and
is also symmetric about this point. In fact, when plotted with the
appropriate ratio of vertical to horizontal scalings, the Gaussian probability
density curve looks rather like the outline of a
bell centered on
![]() . Hence, this curve is sometimes
called a bell curve.
At one standard deviation away from the mean value--that is
. Hence, this curve is sometimes
called a bell curve.
At one standard deviation away from the mean value--that is
![]() --the probability density is
about 61% of its peak value. At two standard deviations away from the mean
value, the probability density is about 13.5% of its peak value.
Finally,
at three standard deviations away from the mean value, the probability
density is only about 1% of its peak value. We conclude
that there is
very little chance that
--the probability density is
about 61% of its peak value. At two standard deviations away from the mean
value, the probability density is about 13.5% of its peak value.
Finally,
at three standard deviations away from the mean value, the probability
density is only about 1% of its peak value. We conclude
that there is
very little chance that ![]() lies more than about three standard deviations
away from its mean value. In other words,
lies more than about three standard deviations
away from its mean value. In other words, ![]() is almost certain to lie in the
relatively narrow range
is almost certain to lie in the
relatively narrow range
![]() .
.
![]() , to a continuous probability density,
, to a continuous probability density,
![]() .
The normalization condition becomes
.
The normalization condition becomes