


Next: Binomial Probability Distribution
Up: Probability Theory
Previous: Two-State System
The branch of mathematics that studies the number of different ways of
arranging things is called combinatorial analysis. We need to know
how many different ways there are of arranging  objects that are made up
of two groups of
objects that are made up
of two groups of  and
and 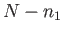 indistinguishable objects. This is a rather
difficult problem. Let us start off by tackling a slightly easier problem.
How many ways are there of arranging
indistinguishable objects. This is a rather
difficult problem. Let us start off by tackling a slightly easier problem.
How many ways are there of arranging  distinguishable
objects? For instance, suppose that we have six pool balls, numbered one
through six, and we pot one each into every one of
the six pockets of a pool table (that is, top-left, top-right, middle-left,
middle-right, bottom-left, and bottom-right). How many different ways
are there of doing this? Let us start with the top-left pocket.
We could pot any one of the six balls into this pocket, so there are
6 possibilities. For the top-right pocket we only have 5 possibilities,
because we have already potted a ball into the top-left pocket, and it
cannot be in two pockets simultaneously. So, our 6 original possibilities
combined with these 5 new possibilities gives
distinguishable
objects? For instance, suppose that we have six pool balls, numbered one
through six, and we pot one each into every one of
the six pockets of a pool table (that is, top-left, top-right, middle-left,
middle-right, bottom-left, and bottom-right). How many different ways
are there of doing this? Let us start with the top-left pocket.
We could pot any one of the six balls into this pocket, so there are
6 possibilities. For the top-right pocket we only have 5 possibilities,
because we have already potted a ball into the top-left pocket, and it
cannot be in two pockets simultaneously. So, our 6 original possibilities
combined with these 5 new possibilities gives 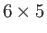 ways of potting
two balls into the top two pockets. For the middle-left pocket we have
4 possibilities, because we have already potted two balls. These possibilities
combined with our
ways of potting
two balls into the top two pockets. For the middle-left pocket we have
4 possibilities, because we have already potted two balls. These possibilities
combined with our 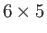 possibilities gives
possibilities gives
 ways
of potting three balls into three pockets.
At this stage, it should be clear that
the final answer is going to be
ways
of potting three balls into three pockets.
At this stage, it should be clear that
the final answer is going to be
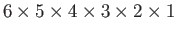 .
The factorial of a general
positive
integer,
.
The factorial of a general
positive
integer,  , is defined
, is defined
 |
(2.17) |
So, 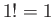 , and
, and
 , and
, and
 , and so on. Clearly, the
number of ways of potting six distinguishable pool balls into six pockets is
, and so on. Clearly, the
number of ways of potting six distinguishable pool balls into six pockets is 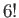 (which
incidentally equals 720). Because there is nothing special about pool balls, or
the number six, we can safely infer that the number of different ways of
arranging
(which
incidentally equals 720). Because there is nothing special about pool balls, or
the number six, we can safely infer that the number of different ways of
arranging  distinguishable objects, denoted
distinguishable objects, denoted 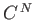 , is given by
, is given by
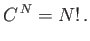 |
(2.18) |
Suppose that we take the number four ball off the pool
table, and replace it
by a second number five ball. How many different ways are there of potting
the balls now? Consider a previous arrangement in which the number five
ball was potted into the top-left pocket, and the number four ball was potted
into the top-right pocket, and then consider a second arrangement that only
differs from the first because the number four and five balls have been
swapped around.
These arrangements are now
indistinguishable, and are therefore counted as a single arrangement, whereas
previously they were counted as two separate arrangements. Clearly, the
previous arrangements can be divided into two groups, containing equal numbers
of arrangements, that differ only by the permutation of the
number four and five balls. Because these balls are now indistinguishable, we
conclude that there are only half as many different arrangements as
there were before. If we take the number three ball off the table, and replace
it by a third number five ball, then we can split the original arrangements into
six equal groups of arrangements that differ only by the permutation
of the number three, four, and five balls. There are six groups because there
are 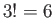 separate permutations of these three balls. Because the number three,
four, and five balls are now indistinguishable, we conclude that there are
only
separate permutations of these three balls. Because the number three,
four, and five balls are now indistinguishable, we conclude that there are
only 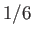 the number of original arrangements. Generalizing this result, we
conclude that the number of arrangements of
the number of original arrangements. Generalizing this result, we
conclude that the number of arrangements of  indistinguishable and
indistinguishable and
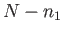 distinguishable objects is
distinguishable objects is
 |
(2.19) |
We can see that if all the balls on the table are replaced by number
five balls then there is only  possible arrangement. This
corresponds, of course, to a number five ball in each pocket.
A further straightforward generalization tells us that the
number of arrangements of two groups of
possible arrangement. This
corresponds, of course, to a number five ball in each pocket.
A further straightforward generalization tells us that the
number of arrangements of two groups of  and
and 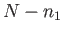 indistinguishable
objects is
indistinguishable
objects is
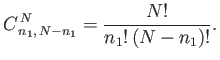 |
(2.20) |



Next: Binomial Probability Distribution
Up: Probability Theory
Previous: Two-State System
Richard Fitzpatrick
2016-01-25
![]() separate permutations of these three balls. Because the number three,
four, and five balls are now indistinguishable, we conclude that there are
only
separate permutations of these three balls. Because the number three,
four, and five balls are now indistinguishable, we conclude that there are
only ![]() the number of original arrangements. Generalizing this result, we
conclude that the number of arrangements of
the number of original arrangements. Generalizing this result, we
conclude that the number of arrangements of ![]() indistinguishable and
indistinguishable and
![]() distinguishable objects is
distinguishable objects is
