


Next: Wave Packets
Up: Wave Mechanics
Previous: Schrödinger's Equation
Probability Interpretation of Wavefunction
After many false starts, physicists in the early 20th century eventually came to the conclusion that the only physical
interpretation of a particle wavefunction that is consistent with experimental observations is probabilistic in nature. To be more exact, if 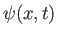 is the
complex wavefunction of a given particle, moving in one dimension along the
is the
complex wavefunction of a given particle, moving in one dimension along the  -axis, then the probability of finding the particle between
-axis, then the probability of finding the particle between  and
and
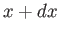 at time
at time  is
is
 |
(C.30) |
We can interpret
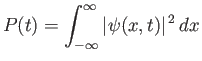 |
(C.31) |
as the probability of the particle being found anywhere between  and
and 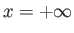 at time
at time  . This follows, via induction,
from the fundamental result in probability theory that the probability of the occurrence of one or other of two mutually exclusive events (such as the particle being found in two
non-overlapping regions) is the sum (or integral) of the probabilities of the individual events. (See Section 2.3.)
Assuming that the
particle exists, it is certain that it will be found somewhere between
. This follows, via induction,
from the fundamental result in probability theory that the probability of the occurrence of one or other of two mutually exclusive events (such as the particle being found in two
non-overlapping regions) is the sum (or integral) of the probabilities of the individual events. (See Section 2.3.)
Assuming that the
particle exists, it is certain that it will be found somewhere between  and
and 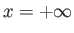 at time
at time  . Because a certain event
has probability
. Because a certain event
has probability 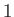 (see Section 2.2), our probability interpretation of the wavefunction is only tenable provided
(see Section 2.2), our probability interpretation of the wavefunction is only tenable provided
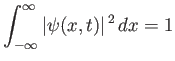 |
(C.32) |
at all times.
A wavefunction that satisfies the previous condition--which is known as the normalization condition--is said to be properly normalized.
Suppose that we have a wavefunction, 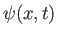 , which is such that it satisfies the normalization condition (C.32)
at time
, which is such that it satisfies the normalization condition (C.32)
at time  . Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (C.24).
Our probability interpretation of the wavefunction only makes sense if the normalization
condition remains satisfied at all subsequent times. This follows because if the particle is certain to be
found somewhere on the
. Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (C.24).
Our probability interpretation of the wavefunction only makes sense if the normalization
condition remains satisfied at all subsequent times. This follows because if the particle is certain to be
found somewhere on the  -axis (which is the interpretation put on the normalization condition) at time
-axis (which is the interpretation put on the normalization condition) at time  then
it is equally certain to be found somewhere on the
then
it is equally certain to be found somewhere on the  -axis at a later time (because we are not considering any
physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that
Schrödinger's equation preserves the normalization of the wavefunction.
-axis at a later time (because we are not considering any
physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that
Schrödinger's equation preserves the normalization of the wavefunction.
Taking Schrödinger's equation, and multiplying it by 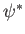 (the complex conjugate of the wavefunction), we
obtain
(the complex conjugate of the wavefunction), we
obtain
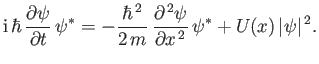 |
(C.33) |
The complex conjugate of the previous expression yields
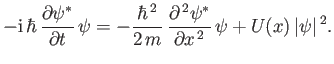 |
(C.34) |
Here, use has been made of the readily demonstrated results
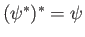 and
and
 , as well as the fact that
, as well as the fact that  is real.
Taking the difference between the previous two expressions, we obtain
is real.
Taking the difference between the previous two expressions, we obtain
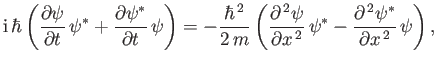 |
(C.35) |
which can be written
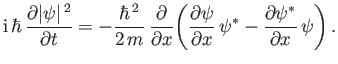 |
(C.36) |
Integrating in  , we get
, we get
![$\displaystyle {\rm i} \hbar \frac{d}{dt}\int_{-\infty}^\infty \vert\psi\vert^...
...\psi^\ast - \frac{\partial\psi^\ast}{\partial x} \psi\right]_{-\infty}^\infty.$](img3129.png) |
(C.37) |
Finally, assuming that the wavefunction is localized in space: that is,
 as as 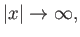 |
(C.38) |
we obtain
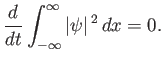 |
(C.39) |
It follows, from the preceding analysis, that if a localized wavefunction is properly normalized at  (i.e., if
(i.e., if
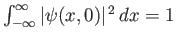 ) then it will remain properly
normalized as it evolves in time according to Schrödinger's equation. Incidentally,
a wavefunction that is not localized cannot be properly normalized, because its normalization integral
) then it will remain properly
normalized as it evolves in time according to Schrödinger's equation. Incidentally,
a wavefunction that is not localized cannot be properly normalized, because its normalization integral
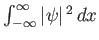 is necessarily infinite. For such a wavefunction,
is necessarily infinite. For such a wavefunction,
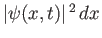 gives the relative, rather than the
absolute, probability of finding the particle between
gives the relative, rather than the
absolute, probability of finding the particle between  and
and 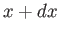 at time
at time  . In other words, [cf., Equation (C.30)]
. In other words, [cf., Equation (C.30)]
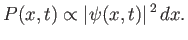 |
(C.40) |



Next: Wave Packets
Up: Wave Mechanics
Previous: Schrödinger's Equation
Richard Fitzpatrick
2016-01-25
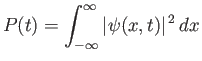
![]() , which is such that it satisfies the normalization condition (C.32)
at time
, which is such that it satisfies the normalization condition (C.32)
at time ![]() . Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (C.24).
Our probability interpretation of the wavefunction only makes sense if the normalization
condition remains satisfied at all subsequent times. This follows because if the particle is certain to be
found somewhere on the
. Furthermore, let the wavefunction evolve in time according to Schrödinger's equation, (C.24).
Our probability interpretation of the wavefunction only makes sense if the normalization
condition remains satisfied at all subsequent times. This follows because if the particle is certain to be
found somewhere on the ![]() -axis (which is the interpretation put on the normalization condition) at time
-axis (which is the interpretation put on the normalization condition) at time ![]() then
it is equally certain to be found somewhere on the
then
it is equally certain to be found somewhere on the ![]() -axis at a later time (because we are not considering any
physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that
Schrödinger's equation preserves the normalization of the wavefunction.
-axis at a later time (because we are not considering any
physical process by which particles can be created or destroyed). Thus, it is necessary for us to demonstrate that
Schrödinger's equation preserves the normalization of the wavefunction.
![]() (the complex conjugate of the wavefunction), we
obtain
(the complex conjugate of the wavefunction), we
obtain
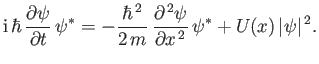
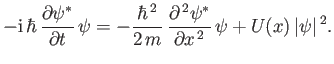
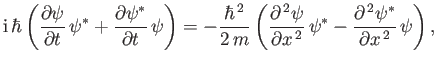
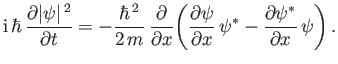
![$\displaystyle {\rm i} \hbar \frac{d}{dt}\int_{-\infty}^\infty \vert\psi\vert^...
...\psi^\ast - \frac{\partial\psi^\ast}{\partial x} \psi\right]_{-\infty}^\infty.$](img3129.png)
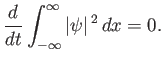
![]() (i.e., if
(i.e., if
![]() ) then it will remain properly
normalized as it evolves in time according to Schrödinger's equation. Incidentally,
a wavefunction that is not localized cannot be properly normalized, because its normalization integral
) then it will remain properly
normalized as it evolves in time according to Schrödinger's equation. Incidentally,
a wavefunction that is not localized cannot be properly normalized, because its normalization integral
![]() is necessarily infinite. For such a wavefunction,
is necessarily infinite. For such a wavefunction,
![]() gives the relative, rather than the
absolute, probability of finding the particle between
gives the relative, rather than the
absolute, probability of finding the particle between ![]() and
and ![]() at time
at time ![]() . In other words, [cf., Equation (C.30)]
. In other words, [cf., Equation (C.30)]