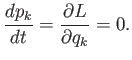Next: Calculus of Variations
Up: Classical Mechanics
Previous: Lagrange's Equation
Generalized Momenta
Consider the motion of a single particle moving in one dimension. The
kinetic energy is
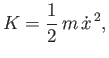 |
(B.23) |
where  is the mass of the particle, and
is the mass of the particle, and  its displacement.
The particle's linear momentum is
its displacement.
The particle's linear momentum is
 . However,
this can also be written
. However,
this can also be written
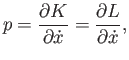 |
(B.24) |
because  , and the potential energy,
, and the potential energy, 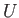 , is independent of
, is independent of 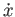 .
.
Consider a dynamical system described by  generalized coordinates,
generalized coordinates,
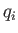 , for
, for
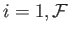 . By analogy with the previous expression, we can
define generalized momenta of the form
. By analogy with the previous expression, we can
define generalized momenta of the form
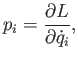 |
(B.25) |
for
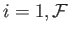 . Here,
. Here,  is sometimes called the momentum conjugate to the coordinate
is sometimes called the momentum conjugate to the coordinate 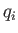 . Hence, Lagrange's equation, (B.22), can be written
. Hence, Lagrange's equation, (B.22), can be written
 |
(B.26) |
for
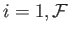 . Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
. Note that a generalized momentum does not necessarily have
the dimensions of linear momentum.
Suppose that the Lagrangian, 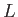 , does not depend explicitly on some coordinate
, does not depend explicitly on some coordinate
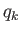 . It follows from Equation (B.26) that
. It follows from Equation (B.26) that
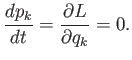 |
(B.27) |
Hence,
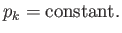 |
(B.28) |
The coordinate 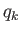 is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.
is said to be ignorable in this case.
Thus, we conclude that the generalized momentum associated with
an ignorable coordinate is a constant of the motion.



Next: Calculus of Variations
Up: Classical Mechanics
Previous: Lagrange's Equation
Richard Fitzpatrick
2016-01-25
![]() generalized coordinates,
generalized coordinates,
![]() , for
, for
![]() . By analogy with the previous expression, we can
define generalized momenta of the form
. By analogy with the previous expression, we can
define generalized momenta of the form
![]() , does not depend explicitly on some coordinate
, does not depend explicitly on some coordinate
![]() . It follows from Equation (B.26) that
. It follows from Equation (B.26) that