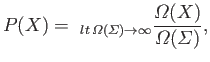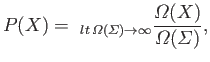Next: Combining Probabilities
Up: Probability Theory
Previous: Introduction
What is Probability?
What is the scientific
definition of probability? Consider
an observation made on a general system, 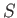 . This can result in
any one of a number
of different possible outcomes. We want to find the probability of
some general outcome,
. This can result in
any one of a number
of different possible outcomes. We want to find the probability of
some general outcome, 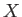 . In order to ascribe a probability, we have to
consider the system as a member of a large set,
. In order to ascribe a probability, we have to
consider the system as a member of a large set,
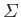 ,
of similar systems.
Mathematicians call such a group an ensemble, which is
just the French for ``group.'' So, let us consider an ensemble,
,
of similar systems.
Mathematicians call such a group an ensemble, which is
just the French for ``group.'' So, let us consider an ensemble,
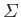 , of
similar systems,
, of
similar systems, 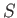 . The probability of the outcome
. The probability of the outcome 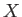 is defined as the
ratio of the number of systems in the ensemble that exhibit this outcome
to the total number of systems, in the limit where the latter
number tends to
infinity. We can write this symbolically as
is defined as the
ratio of the number of systems in the ensemble that exhibit this outcome
to the total number of systems, in the limit where the latter
number tends to
infinity. We can write this symbolically as
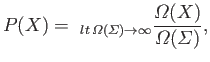 |
(2.1) |
where
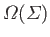 is the total number of systems in the ensemble,
and
is the total number of systems in the ensemble,
and
 the
number of systems exhibiting the outcome
the
number of systems exhibiting the outcome 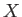 . We can see that the probability,
. We can see that the probability,
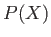 , must be a number lying between 0 and 1. The probability is zero if no
systems exhibit the outcome
, must be a number lying between 0 and 1. The probability is zero if no
systems exhibit the outcome 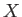 , even when the number of systems goes to
infinity. This is just another way of saying that the
outcome
, even when the number of systems goes to
infinity. This is just another way of saying that the
outcome 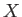 is impossible. The probability is unity if all systems exhibit the outcome
is impossible. The probability is unity if all systems exhibit the outcome
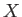 , in the limit that the number of systems goes to infinity. This is another
way of saying that the outcome
, in the limit that the number of systems goes to infinity. This is another
way of saying that the outcome 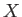 is bound to occur.
is bound to occur.



Next: Combining Probabilities
Up: Probability Theory
Previous: Introduction
Richard Fitzpatrick
2016-01-25