- Show that the properly normalized probability that the
volume lies between
 and
and 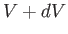 , and the temperature lies between
, and the temperature lies between  and
and 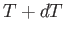 , is
, is
![$\displaystyle P(V, T) dV dT = \frac{1}{2\pi {\mit\Delta}^\ast V {\mit\Delta...
...t[-\frac{(T-\overline{T})^{ 2}}{2 ({\mit\Delta}^\ast T)^{ 2}}\right]dV dT,
$](img2787.png)
where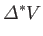

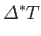
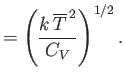
Here, the mean temperature,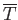 , is the same as that of the remainder of the substance, whereas the mean volume,
, is the same as that of the remainder of the substance, whereas the mean volume,
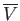 , is
such that when
, is
such that when
 the pressure of the region matches that of the surrounding substance.
the pressure of the region matches that of the surrounding substance.
- Hence, deduce that
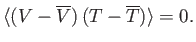
In other words, the volume and temperature fluctuations are uncorrelated. - Show that for the case of a monatomic ideal gas
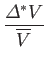


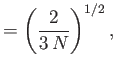
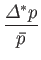
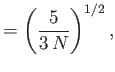
where is the pressure of the region. Furthermore, demonstrate that
is the pressure of the region. Furthermore, demonstrate that
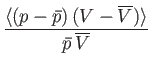
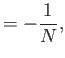
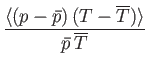
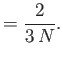

- Deduce that the triple point of ammonia occurs at
 K.
K.
- Show that, at the triple point, the latent heats of sublimation, vaporization, and melting of ammonia are
 ,
,
 , and
, and
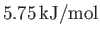 , respectively.
, respectively.
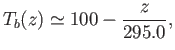
where
![$\displaystyle T_d \simeq T-\frac{R T^{ 2}}{l} \ln\left[\frac{1}{h(T)}\right].
$](img2822.png)
Here,
- Use the first law of thermodynamics to show that, as condensation forms during adiabatic expansion, the temperature
of the air mass changes by
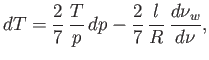
where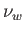 is the number of moles of water vapor,
is the number of moles of water vapor, 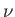 the total number of moles, and
the total number of moles, and 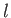 the molar latent heat of vaporization of water.
Here, we have assumed that
the molar latent heat of vaporization of water.
Here, we have assumed that
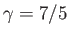 for air.
for air.
- Assuming that the air is always saturated during this process, show that

where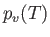 is the vapor pressure of water at temperature
is the vapor pressure of water at temperature  , and
, and  is the pressure of the atmosphere.
is the pressure of the atmosphere.
- Use the equation of hydrostatic equilibrium of the atmosphere,
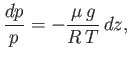
where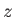 represents altitude,
represents altitude,  is the molecular weight of air, and
is the molecular weight of air, and 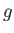 the acceleration due to gravity, to obtain the following expression
so-called wet adiabatic lapse-rate of the atmosphere:
the acceleration due to gravity, to obtain the following expression
so-called wet adiabatic lapse-rate of the atmosphere:
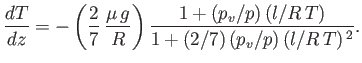
Of course,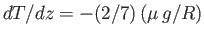 is the dry adiabatic lapse-rate derived in Section 6.8.
is the dry adiabatic lapse-rate derived in Section 6.8.
- At
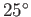 C, the vapor pressure of water is
C, the vapor pressure of water is  bar, and the molar latent heat of vaporization is
bar, and the molar latent heat of vaporization is
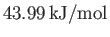 . At
. At  C, the vapor pressure of water is
C, the vapor pressure of water is 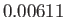 bar, and the molar latent heat of vaporization is
bar, and the molar latent heat of vaporization is
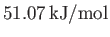 . What is the ratio of the wet adiabatic lapse-rate to the dry adiabatic lapse-rate at these two temperatures?
. What is the ratio of the wet adiabatic lapse-rate to the dry adiabatic lapse-rate at these two temperatures?

Let
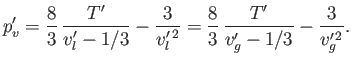
Moreover, the Maxwell construction yields
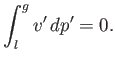
- Demonstrate that the Maxwell construction implies that

- Eliminate
 and
and 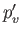 from the previous equations to obtain the transcendental equation
from the previous equations to obtain the transcendental equation

that relates the molar volumes of the liquid and gas phases. - Writing
 and
and
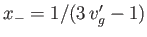 , show that the previous equation reduces to
, show that the previous equation reduces to
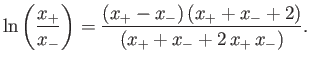
- By setting both sides of the previous equation equal to
 , show that it can be solved parametrically to give
, show that it can be solved parametrically to give
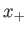
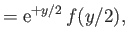
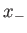
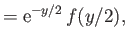
where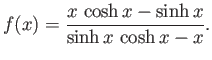
- Furthermore, demonstrate that
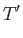
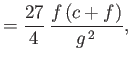
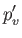
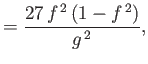
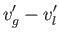

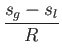
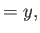
where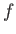
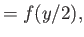
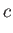

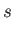
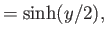
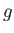
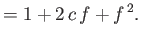
Here, and
and 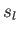 denote the molar entropies of the gas and liquid phases, respectively.
denote the molar entropies of the gas and liquid phases, respectively.
- Finally, by considering the limits
 and
and 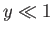 , show that
, show that
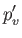
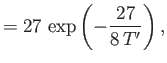
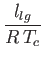
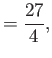
in the limit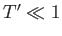 , and
, and
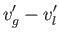
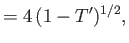
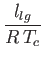

in the limit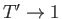 . Here,
. Here, 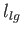 is the molar latent heat of vaporization.
is the molar latent heat of vaporization.