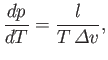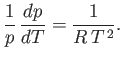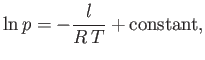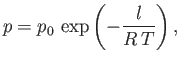Next: Phase Transformations in Van
Up: Multi-Phase Systems
Previous: Phase Diagrams
The Clausius-Clapeyron equation can be used to derive an approximate expression for the pressure of the vapor
in equilibrium with the liquid (or solid) at some temperature  . This pressure is called the vapor pressure
of the liquid (or solid) at this temperature. According to Equation (9.74),
. This pressure is called the vapor pressure
of the liquid (or solid) at this temperature. According to Equation (9.74),
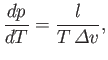 |
(9.75) |
where 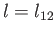 is the latent heat per mole, and
is the latent heat per mole, and  the molar volume. Let
the molar volume. Let 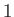 refer to the liquid
(or solid) phase, and
refer to the liquid
(or solid) phase, and 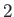 to the vapor. It follows that
to the vapor. It follows that
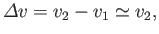 |
(9.76) |
because the vapor is much less dense than the liquid, so that
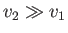 . Let us also
assume that the vapor can be adequately treated as an ideal gas, so that its equation of state is
written
. Let us also
assume that the vapor can be adequately treated as an ideal gas, so that its equation of state is
written
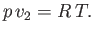 |
(9.77) |
Thus,
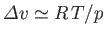 , and Equation (9.75) becomes
, and Equation (9.75) becomes
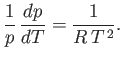 |
(9.78) |
Assuming that 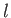 is approximately temperature independent, we can integrate the previous equation to give
is approximately temperature independent, we can integrate the previous equation to give
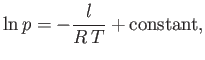 |
(9.79) |
which implies that
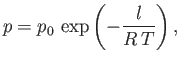 |
(9.80) |
where 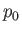 is some constant. This result shows that the vapor pressure,
is some constant. This result shows that the vapor pressure,  , is a very rapidly increasing function of the
temperature,
, is a very rapidly increasing function of the
temperature,  .
.



Next: Phase Transformations in Van
Up: Multi-Phase Systems
Previous: Phase Diagrams
Richard Fitzpatrick
2016-01-25