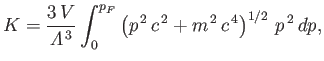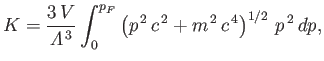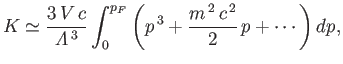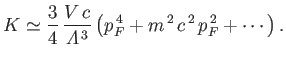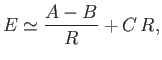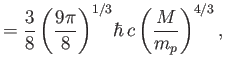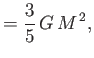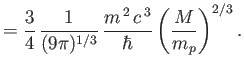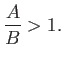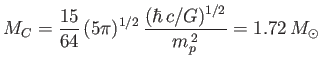Next: Neutron Stars
Up: Quantum Statistics
Previous: White-Dwarf Stars
One curious feature of white-dwarf stars is that their radius decreases
as their mass increases. [See Equation (8.206).] It follows, from Equation (8.199),
that the mean energy of the degenerate electrons inside the
star increases strongly as the stellar
mass increases: in fact,
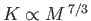 . Hence, if
. Hence, if
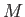 becomes sufficiently large then the electrons become relativistic, and
the previous analysis needs to be modified. Strictly speaking, the non-relativistic
analysis described in the previous section
is only valid in the low-mass limit
becomes sufficiently large then the electrons become relativistic, and
the previous analysis needs to be modified. Strictly speaking, the non-relativistic
analysis described in the previous section
is only valid in the low-mass limit
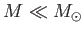 .
Let us, for the sake of simplicity, consider the ultra-relativistic
limit in which
.
Let us, for the sake of simplicity, consider the ultra-relativistic
limit in which  .
.
The total electron energy (including the rest mass energy) can be
written
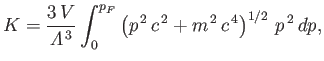 |
(8.207) |
by analogy with Equation (8.198). Thus,
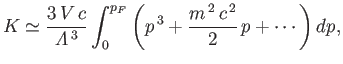 |
(8.208) |
giving
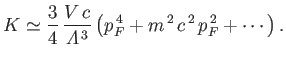 |
(8.209) |
It follows, from the previous analysis, that the total energy of an ultra-relativistic
white-dwarf star can be written
in the
form
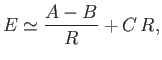 |
(8.210) |
where
As before, the equilibrium radius 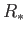 is that which minimizes the
total energy.
is that which minimizes the
total energy.  .
However, in the ultra-relativistic case, a non-zero value of
.
However, in the ultra-relativistic case, a non-zero value of 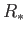 only exists
for
only exists
for 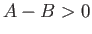 . When
. When 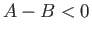 , the energy decreases monotonically with decreasing
stellar radius. In other words, the degeneracy pressure
of the electrons is incapable of halting the collapse of the star under gravity.
The criterion that must be satisfied for a relativistic white-dwarf
star to be maintained against gravity is that
, the energy decreases monotonically with decreasing
stellar radius. In other words, the degeneracy pressure
of the electrons is incapable of halting the collapse of the star under gravity.
The criterion that must be satisfied for a relativistic white-dwarf
star to be maintained against gravity is that
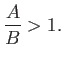 |
(8.214) |
This criterion can be re-written
 |
(8.215) |
where
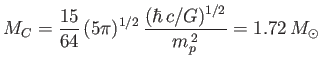 |
(8.216) |
is known as the Chandrasekhar limit, after A. Chandrasekhar
who first derived it in 1931.
A more realistic calculation, which does not assume constant density,
yields
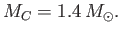 |
(8.217) |
Thus, if the stellar mass exceeds the Chandrasekhar limit then the star in question
cannot become a white-dwarf when its nuclear fuel is exhausted, but, instead,
must continue to
collapse. What is the ultimate fate of such a star?



Next: Neutron Stars
Up: Quantum Statistics
Previous: White-Dwarf Stars
Richard Fitzpatrick
2016-01-25