


Next: Stefan-Boltzmann Law
Up: Quantum Statistics
Previous: Planck Radiation Law
Suppose that we were to make a small hole in the wall of our enclosure,
and observe the emitted radiation. A small hole is the best approximation in
physics to a black-body, which is defined as an object that absorbs, and,
therefore, emits, radiation perfectly at all wavelengths.
What is the power radiated by the hole? Well, the power density inside the enclosure
can be written
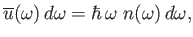 |
(8.119) |
where 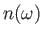 is the mean
number of photons per unit volume whose frequencies lie
in the range
is the mean
number of photons per unit volume whose frequencies lie
in the range  to
to
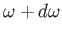 . The radiation field inside the
enclosure is isotropic (we are assuming that the hole is sufficiently small that
it does not distort the field). It follows that the mean number of photons
per unit volume
whose frequencies lie in the specified range, and
whose directions of propagation make an angle in the range
. The radiation field inside the
enclosure is isotropic (we are assuming that the hole is sufficiently small that
it does not distort the field). It follows that the mean number of photons
per unit volume
whose frequencies lie in the specified range, and
whose directions of propagation make an angle in the range
 to
to
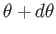 with the normal to the hole, is
with the normal to the hole, is
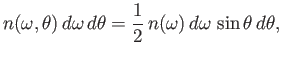 |
(8.120) |
where
 is proportional to the solid angle in the specified
range of directions,
and
is proportional to the solid angle in the specified
range of directions,
and
 |
(8.121) |
Photons travel at the velocity of light, so the power per unit area escaping from
the hole in the frequency range  to
to
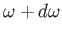 is
is
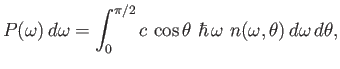 |
(8.122) |
where
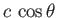 is the component of the photon velocity in the direction
of the hole.
This gives
is the component of the photon velocity in the direction
of the hole.
This gives
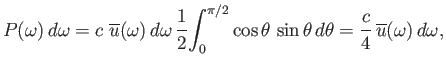 |
(8.123) |
so
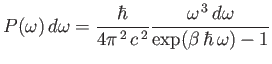 |
(8.124) |
is the power per unit area radiated by a black-body in the frequency range
 to
to
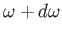 .
.
A black-body is very much an idealization. The power
spectra of real radiating bodies
can deviate quite substantially from black-body spectra. Nevertheless, we
can make some useful predictions using this model. The black-body power spectrum
peaks when
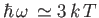 . (See Exercise 15.) This means that the peak radiation
frequency scales linearly with the temperature of the body. In other words,
hot bodies tend to radiate at higher frequencies than cold bodies. This
result (in particular, the linear scaling) is known as Wien's displacement
law. It allows us to estimate the surface temperatures of stars from their
colors (surprisingly enough, stars are fairly good black-bodies). Table 8.4 shows
some stellar temperatures determined by this method (in fact,
the whole emission spectrum is fitted to a black-body spectrum).
It can be seen that the
apparent colors (which correspond quite well to the colors of the peak radiation)
scan the whole visible spectrum, from red to blue, as the stellar surface temperatures
gradually rise.
. (See Exercise 15.) This means that the peak radiation
frequency scales linearly with the temperature of the body. In other words,
hot bodies tend to radiate at higher frequencies than cold bodies. This
result (in particular, the linear scaling) is known as Wien's displacement
law. It allows us to estimate the surface temperatures of stars from their
colors (surprisingly enough, stars are fairly good black-bodies). Table 8.4 shows
some stellar temperatures determined by this method (in fact,
the whole emission spectrum is fitted to a black-body spectrum).
It can be seen that the
apparent colors (which correspond quite well to the colors of the peak radiation)
scan the whole visible spectrum, from red to blue, as the stellar surface temperatures
gradually rise.
Table 8.4:
Physical properties of some well-known stars.
| Name |
Constellation |
Spectral Type |
Surface Temp. (K) |
Color |
| Antares |
Scorpio |
M |
3300 |
Very Red |
| Aldebaran |
Taurus |
K |
3800 |
Reddish Yellow |
| Sun |
|
G |
5770 |
Yellow |
| Procyon |
Canis Minor |
F |
6570 |
Yellowish White |
| Sirius |
Canis Major |
A |
9250 |
White |
| Rigel |
Orion |
B |
11,200 |
Bluish White |
|
Probably the most famous black-body spectrum is cosmological in origin. Just after
the ``big bang,'' the universe was essentially a ``fireball,'' with the energy associated with
radiation completely dominating that associated with
matter. The early universe was also fairly
well described by equilibrium statistical thermodynamics,
which means that the radiation had a black-body spectrum. As the universe expanded,
the radiation was gradually Doppler shifted to ever larger wavelengths (in other
words, the radiation did work against the expansion of the universe, and, thereby,
lost energy--see Exercise 13), but its spectrum remained invariant. Nowadays, this primordial
radiation is detectable as a faint microwave background that pervades the
whole universe. The microwave background was discovered accidentally by Penzias
and Wilson in 1961. Until recently, it was difficult to measure the full
spectrum with any degree of
precision, because of strong microwave absorption and scattering by
the Earth's atmosphere. However, all of this changed when the COBE satellite
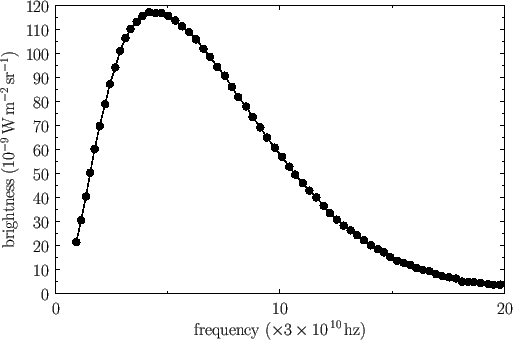
was launched in 1989. It took precisely nine minutes to measure the perfect
black-body spectrum reproduced in Figure 8.3.
This data can be fitted to a black-body
curve of characteristic
temperature 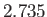 K. In a very real sense, this can be regarded
as the ``temperature of the universe.''
K. In a very real sense, this can be regarded
as the ``temperature of the universe.''
Figure:
Cosmic background radiation spectrum measured by the
Far Infrared Absolute Spectrometer (FIRAS) aboard the Cosmic Background
Explorer satellite (COBE). The fit is to a black-body spectrum of characteristic temperature
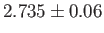 K.
[Data from J.C. Mather, et al., Astrophysical Journal Letters 354, L37 (1990).]
K.
[Data from J.C. Mather, et al., Astrophysical Journal Letters 354, L37 (1990).]
 |



Next: Stefan-Boltzmann Law
Up: Quantum Statistics
Previous: Planck Radiation Law
Richard Fitzpatrick
2016-01-25
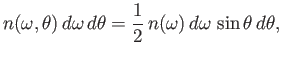

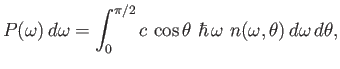
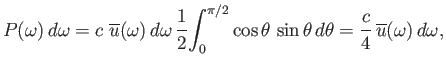
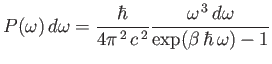
![]() . (See Exercise 15.) This means that the peak radiation
frequency scales linearly with the temperature of the body. In other words,
hot bodies tend to radiate at higher frequencies than cold bodies. This
result (in particular, the linear scaling) is known as Wien's displacement
law. It allows us to estimate the surface temperatures of stars from their
colors (surprisingly enough, stars are fairly good black-bodies). Table 8.4 shows
some stellar temperatures determined by this method (in fact,
the whole emission spectrum is fitted to a black-body spectrum).
It can be seen that the
apparent colors (which correspond quite well to the colors of the peak radiation)
scan the whole visible spectrum, from red to blue, as the stellar surface temperatures
gradually rise.
. (See Exercise 15.) This means that the peak radiation
frequency scales linearly with the temperature of the body. In other words,
hot bodies tend to radiate at higher frequencies than cold bodies. This
result (in particular, the linear scaling) is known as Wien's displacement
law. It allows us to estimate the surface temperatures of stars from their
colors (surprisingly enough, stars are fairly good black-bodies). Table 8.4 shows
some stellar temperatures determined by this method (in fact,
the whole emission spectrum is fitted to a black-body spectrum).
It can be seen that the
apparent colors (which correspond quite well to the colors of the peak radiation)
scan the whole visible spectrum, from red to blue, as the stellar surface temperatures
gradually rise.
![]() K. In a very real sense, this can be regarded
as the ``temperature of the universe.''
K. In a very real sense, this can be regarded
as the ``temperature of the universe.''
