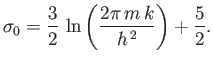Next: Derivation of van der
Up: Quantum Statistics
Previous: Quantum Statistics in Classical
Quantum-Mechanical Treatment of Ideal Gas
Let us calculate the partition function of an ideal gas from quantum mechanics, making use of
Maxwell-Boltzmann statistics. Obviously, such a partition function is only applicable when the gas is non-degenerate. According to Equations (8.67)
and (8.69), we
can write the partition function in the form
 |
(8.70) |
where  is the number of constituent molecules,
is the number of constituent molecules,
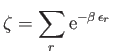 |
(8.71) |
is the partition function of an individual molecule, and the factor 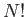 is necessary to take into account the
fact that the molecules are indistinguishable according to quantum theory.
is necessary to take into account the
fact that the molecules are indistinguishable according to quantum theory.
Suppose that the gas is enclosed in a parallelepiped with sides of lengths 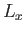 ,
, 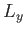 , and
, and 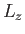 . It follows that
the de Broglie wavenumbers of the constituent molecules are quantized such that
. It follows that
the de Broglie wavenumbers of the constituent molecules are quantized such that
where 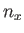 ,
, 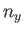 , and
, and 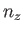 are independent integers. (See Section C.10.) Thus, the allowed energy levels
of a single molecule are
are independent integers. (See Section C.10.) Thus, the allowed energy levels
of a single molecule are
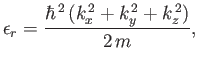 |
(8.75) |
where  is the molecular mass.
Hence, we deduce that
is the molecular mass.
Hence, we deduce that
![$\displaystyle \zeta =\sum_{k_x,k_y,k_z}\exp\left[-\frac{\beta \hbar^{ 2}}{2 m} (k_x^{ 2}+k_y^{ 2}+k_z^{ 2})\right],$](img2106.png) |
(8.76) |
where the sum is over all possible values of  ,
, 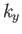 ,
, 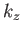 . The previous expression can also be
written
. The previous expression can also be
written
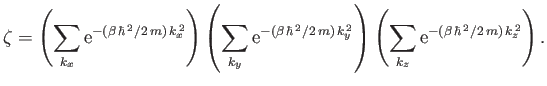 |
(8.77) |
Now, in the previous equation, the successive terms in the sum over  (say) correspond to a very small increment,
(say) correspond to a very small increment,
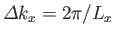 , in
, in  (in fact, the increment can be made arbitrarily small
by increasing
(in fact, the increment can be made arbitrarily small
by increasing 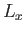 ), and, therefore, differ very little from each other. Hence, it is an
excellent approximation to replace the sums in Equation (8.77) by integrals.
Given that
), and, therefore, differ very little from each other. Hence, it is an
excellent approximation to replace the sums in Equation (8.77) by integrals.
Given that
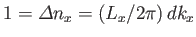 , we can write
, we can write
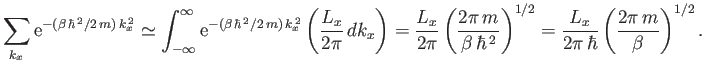 |
(8.78) |
(See Exercise 2.)
Hence, Equation (8.77) becomes
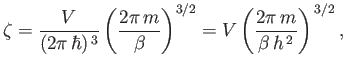 |
(8.79) |
where
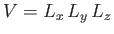 is the volume of the gas.
is the volume of the gas.
It follows from Equation (8.70) that
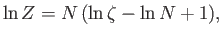 |
(8.80) |
where use has been made of Stirling's approximation. Thus, we obtain
![$\displaystyle \ln Z =N\left[\ln \left(\frac{V}{N}\right) -\frac{3}{2} \ln\beta +\frac{3}{2} \ln\left(\frac{2\pi m}{h^{ 2}}\right)+1 \right],$](img2113.png) |
(8.81) |
and
 |
(8.82) |
and, finally,
![$\displaystyle S = k\left(\ln Z+\beta \overline{E}\right) = N k \left[\ln \left(\frac{V}{N}\right) +\frac{3}{2} \ln T +\sigma_0 \right],$](img2115.png) |
(8.83) |
where
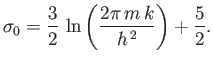 |
(8.84) |
These results are exactly the same as those
obtained in Sections 7.7 and 7.8, using classical mechanics, except that the
arbitrary parameter  is replaced by Planck's constant,
is replaced by Planck's constant,
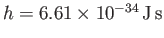 .
.



Next: Derivation of van der
Up: Quantum Statistics
Previous: Quantum Statistics in Classical
Richard Fitzpatrick
2016-01-25

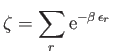
![]() ,
, ![]() , and
, and ![]() . It follows that
the de Broglie wavenumbers of the constituent molecules are quantized such that
. It follows that
the de Broglie wavenumbers of the constituent molecules are quantized such that
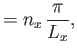
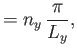

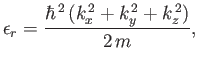
![$\displaystyle \zeta =\sum_{k_x,k_y,k_z}\exp\left[-\frac{\beta \hbar^{ 2}}{2 m} (k_x^{ 2}+k_y^{ 2}+k_z^{ 2})\right],$](img2106.png)
![]() (say) correspond to a very small increment,
(say) correspond to a very small increment,
![]() , in
, in ![]() (in fact, the increment can be made arbitrarily small
by increasing
(in fact, the increment can be made arbitrarily small
by increasing ![]() ), and, therefore, differ very little from each other. Hence, it is an
excellent approximation to replace the sums in Equation (8.77) by integrals.
Given that
), and, therefore, differ very little from each other. Hence, it is an
excellent approximation to replace the sums in Equation (8.77) by integrals.
Given that
![]() , we can write
, we can write
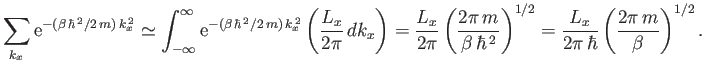
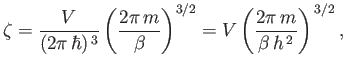
![$\displaystyle \ln Z =N\left[\ln \left(\frac{V}{N}\right) -\frac{3}{2} \ln\beta +\frac{3}{2} \ln\left(\frac{2\pi m}{h^{ 2}}\right)+1 \right],$](img2113.png)

![$\displaystyle S = k\left(\ln Z+\beta \overline{E}\right) = N k \left[\ln \left(\frac{V}{N}\right) +\frac{3}{2} \ln T +\sigma_0 \right],$](img2115.png)