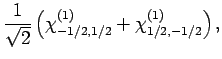Next: Exercises
Up: Addition of Angular Momentum
Previous: Angular Momentum in the
Two Spin One-Half Particles
Consider a system consisting of two spin one-half particles. Suppose
that the system does not possess any orbital angular momentum.
Let  and
and  be the spin angular momentum operators
of the first and second particles, respectively, and let
be the spin angular momentum operators
of the first and second particles, respectively, and let
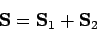 |
(839) |
be the total spin angular momentum operator. By analogy
with the previous analysis, we conclude that it is possible to simultaneously measure either
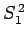 ,
,  ,
, 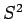 , and
, and  , or
, or
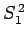 ,
,  ,
, 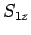 ,
,  , and
, and  .
Let the quantum numbers associated with measurements of
.
Let the quantum numbers associated with measurements of
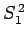 ,
, 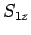 ,
,  ,
,  ,
, 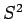 , and
, and
 be
be 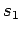 ,
,  ,
, 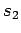 ,
, 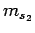 ,
, 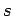 , and
, and 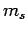 , respectively.
In other words, if the spinor
, respectively.
In other words, if the spinor
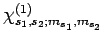 is
a simultaneous eigenstate of
is
a simultaneous eigenstate of 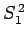 ,
,  ,
, 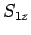 ,
and
,
and  , then
, then
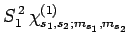 |
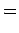 |
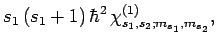 |
(840) |
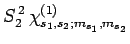 |
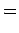 |
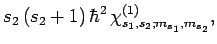 |
(841) |
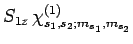 |
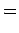 |
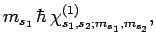 |
(842) |
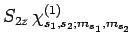 |
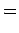 |
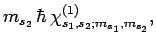 |
(843) |
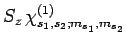 |
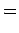 |
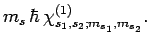 |
(844) |
Likewise, if the spinor
 is
a simultaneous eigenstate of
is
a simultaneous eigenstate of 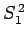 ,
,  ,
, 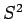 ,
and
,
and  , then
, then
Of course, since both particles have spin one-half, 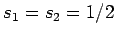 , and
, and
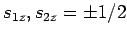 . Furthermore, by analogy with previous
analysis,
. Furthermore, by analogy with previous
analysis,
 |
(849) |
Now, we saw, in the previous section, that when spin 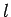 is added
to spin one-half then the possible values of the total angular momentum
quantum number are
is added
to spin one-half then the possible values of the total angular momentum
quantum number are 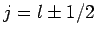 . By analogy, when spin one-half
is added to spin one-half then the possible values of the
total spin quantum number are
. By analogy, when spin one-half
is added to spin one-half then the possible values of the
total spin quantum number are  . In other words,
when two spin one-half particles are combined, we either obtain
a state with overall spin
. In other words,
when two spin one-half particles are combined, we either obtain
a state with overall spin 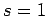 , or a state with overall spin
, or a state with overall spin 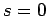 . To be more exact, there are
three possible
. To be more exact, there are
three possible 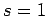 states (corresponding to
states (corresponding to 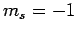 , 0, 1), and
one possible
, 0, 1), and
one possible 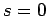 state (corresponding to
state (corresponding to 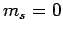 ). The three
). The three 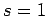 states
are generally known as the triplet states, whereas the
states
are generally known as the triplet states, whereas the
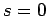 state is known as the singlet state.
state is known as the singlet state.
Table 4:
Clebsch-Gordon coefficients for adding spin one-half to
spin one-half. Only non-zero coefficients are shown.
|
|
The Clebsch-Gordon coefficients for adding spin one-half to
spin one-half can easily be inferred from Table 2 (with 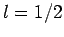 ),
and are listed in Table 4. It follows from this table that the
three triplet states are:
),
and are listed in Table 4. It follows from this table that the
three triplet states are:
where
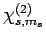 is shorthand for
is shorthand for
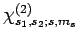 ,
etc. Likewise, the singlet
state is written:
,
etc. Likewise, the singlet
state is written:
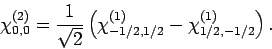 |
(853) |
Subsections



Next: Exercises
Up: Addition of Angular Momentum
Previous: Angular Momentum in the
Richard Fitzpatrick
2010-07-20
![]() is added
to spin one-half then the possible values of the total angular momentum
quantum number are
is added
to spin one-half then the possible values of the total angular momentum
quantum number are ![]() . By analogy, when spin one-half
is added to spin one-half then the possible values of the
total spin quantum number are
. By analogy, when spin one-half
is added to spin one-half then the possible values of the
total spin quantum number are ![]() . In other words,
when two spin one-half particles are combined, we either obtain
a state with overall spin
. In other words,
when two spin one-half particles are combined, we either obtain
a state with overall spin ![]() , or a state with overall spin
, or a state with overall spin ![]() . To be more exact, there are
three possible
. To be more exact, there are
three possible ![]() states (corresponding to
states (corresponding to ![]() , 0, 1), and
one possible
, 0, 1), and
one possible ![]() state (corresponding to
state (corresponding to ![]() ). The three
). The three ![]() states
are generally known as the triplet states, whereas the
states
are generally known as the triplet states, whereas the
![]() state is known as the singlet state.
state is known as the singlet state.
![]() ),
and are listed in Table 4. It follows from this table that the
three triplet states are:
),
and are listed in Table 4. It follows from this table that the
three triplet states are: