


Next: Spin Angular Momentum
Up: Rydberg Formula
Previous: Rydberg Formula
- A particle of mass
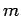 is placed in a finite spherical
well:
is placed in a finite spherical
well:
with 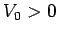 and
and 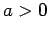 .
Find the ground-state by solving the radial equation with
.
Find the ground-state by solving the radial equation with 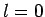 .
Show that there is no ground-state if
.
Show that there is no ground-state if
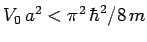 .
.
- Consider a particle of mass
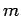 in the three-dimensional harmonic oscillator potential
in the three-dimensional harmonic oscillator potential
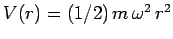 . Solve the problem by separation of
variables in spherical polar coordinates, and, hence, determine the
energy eigenvalues of the system.
. Solve the problem by separation of
variables in spherical polar coordinates, and, hence, determine the
energy eigenvalues of the system.
- The normalized wavefunction for the ground-state of a hydrogen-like
atom (neutral hydrogen,
 ,
, 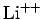 , etc.) with
nuclear charge
, etc.) with
nuclear charge 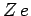 has the form
has the form
where  and
and 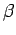 are constants, and
are constants, and 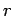 is the distance between the
nucleus and the electron. Show the following:
is the distance between the
nucleus and the electron. Show the following:
-
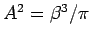 .
.
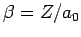 , where
, where
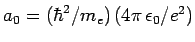 .
.
- The energy is
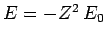 where
where
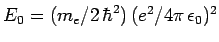 .
.
- The expectation values of the potential and kinetic energies are
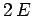 and
and 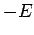 , respectively.
, respectively.
- The expectation value of
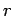 is
is
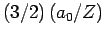 .
.
- The most probable value of
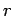 is
is 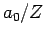 .
.
- An atom of tritium is in its ground-state. Suddenly the nucleus
decays into a helium nucleus, via the emission of a fast electron
which leaves the atom without perturbing the extranuclear electron,
Find the probability that the resulting
 ion will be
left in an
ion will be
left in an 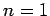 ,
, 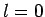 state. Find the probability that it will
be left in a
state. Find the probability that it will
be left in a 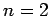 ,
, 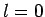 state. What is the probability that the
ion will be left in an
state. What is the probability that the
ion will be left in an 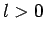 state?
state?
- Calculate the wavelengths of the photons emitted from the
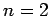 ,
, 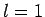 to
to 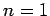 ,
, 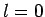 transition in hydrogen, deuterium, and positronium.
transition in hydrogen, deuterium, and positronium.
- To conserve linear momentum, an atom emitting a photon must
recoil, which means that not all of the energy made available in the
downward jump goes to the photon. Find a hydrogen atom's recoil
energy when it emits a photon in an
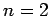 to
to 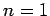 transition. What
fraction of the transition energy is the recoil energy?
transition. What
fraction of the transition energy is the recoil energy?



Next: Spin Angular Momentum
Up: Rydberg Formula
Previous: Rydberg Formula
Richard Fitzpatrick
2010-07-20

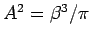 .
.
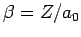 , where
, where
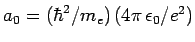 .
.
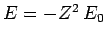 where
where
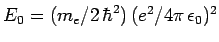 .
.
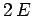 and
and 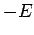 , respectively.
, respectively.
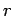 is
is
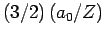 .
.
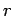 is
is 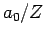 .
.
