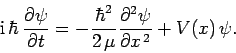Next: Identical Particles
Up: Multi-Particle Systems
Previous: Non-Interacting Particles
Two-Particle Systems
Consider a system consisting of two particles, mass 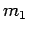 and
and 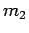 ,
interacting via the potential
,
interacting via the potential 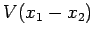 which only depends on the
relative positions of the particles. According to Eqs. (419)
and (426), the Hamiltonian of the system is written
which only depends on the
relative positions of the particles. According to Eqs. (419)
and (426), the Hamiltonian of the system is written
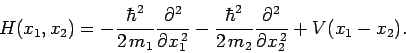 |
(437) |
Let
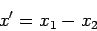 |
(438) |
be the particles' relative position, and
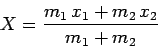 |
(439) |
the position of the center of mass.
It is easily demonstrated that
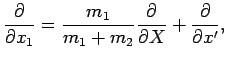 |
|
|
(440) |
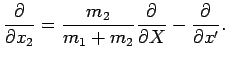 |
|
|
(441) |
Hence, when expressed in terms of the new variables, 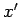 and
and 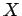 ,
the Hamiltonian becomes
,
the Hamiltonian becomes
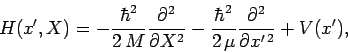 |
(442) |
where
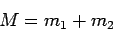 |
(443) |
is the total mass of the system, and
 |
(444) |
the so-called reduced mass.
Note that the total momentum of the system can be written
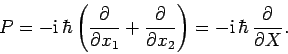 |
(445) |
The fact that the Hamiltonian (442) is separable when expressed
in terms of the new coordinates [i.e.,
![$H(x',X) = H_{x'}(x') + H_X(X)]$](img1121.png) suggests, by analogy with the analysis
in the previous section, that the wavefunction can be factorized: i.e.,
suggests, by analogy with the analysis
in the previous section, that the wavefunction can be factorized: i.e.,
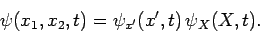 |
(446) |
Hence, the time-dependent Schrödinger equation (423)
also factorizes to give
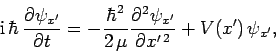 |
(447) |
and
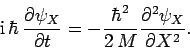 |
(448) |
The above equation can be solved to give
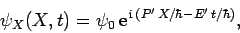 |
(449) |
where 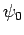 ,
,  , and
, and
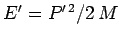 are constants. It is clear, from Eqs. (445), (446), and (449), that
the total momentum of the system takes the constant value
are constants. It is clear, from Eqs. (445), (446), and (449), that
the total momentum of the system takes the constant value  :
i.e., momentum is conserved.
:
i.e., momentum is conserved.
Suppose that we work in the centre of mass frame of the system, which is characterized by
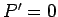 . It follows that
. It follows that
 . In this case, we can write the wavefunction of the system in the form
. In this case, we can write the wavefunction of the system in the form
 , where
, where
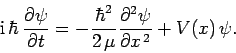 |
(450) |
In other words, in the center of mass frame, two particles of mass 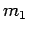 and
and 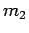 , moving in the potential
, moving in the potential 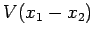 , are equivalent
to a single particle of mass
, are equivalent
to a single particle of mass  , moving in the potential
, moving in the potential 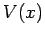 ,
where
,
where 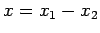 . This is a familiar result from classical dynamics.
. This is a familiar result from classical dynamics.



Next: Identical Particles
Up: Multi-Particle Systems
Previous: Non-Interacting Particles
Richard Fitzpatrick
2010-07-20
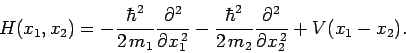
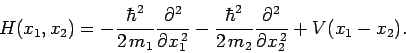
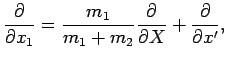
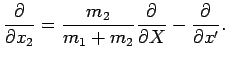
![]() suggests, by analogy with the analysis
in the previous section, that the wavefunction can be factorized: i.e.,
suggests, by analogy with the analysis
in the previous section, that the wavefunction can be factorized: i.e.,
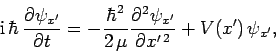
![]() . It follows that
. It follows that
![]() . In this case, we can write the wavefunction of the system in the form
. In this case, we can write the wavefunction of the system in the form
![]() , where
, where