


Next: Forbidden Transitions
Up: Time-Dependent Perturbation Theory
Previous: Transitions in Hydrogen
Now, we know, from Sect. 12.8, that when we take electron spin
and spin-orbit coupling into account the degeneracy of the six  states of the hydrogen atom is broken. In fact, these states are divided
into two groups with slightly different energies. There are four states
characterized by the overall angular momentum quantum number
states of the hydrogen atom is broken. In fact, these states are divided
into two groups with slightly different energies. There are four states
characterized by the overall angular momentum quantum number
 --these are called the
--these are called the 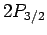 states. The remaining two
states are characterized by
states. The remaining two
states are characterized by 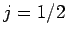 , and are thus called the
, and are thus called the 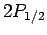 states.
The energy of the
states.
The energy of the 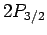 states is slightly higher than that of
the
states is slightly higher than that of
the 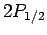 states. In fact, the energy difference
is
states. In fact, the energy difference
is
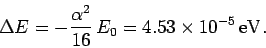 |
(1162) |
Thus, the wavelength of the spectral line associated with the
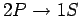 transition
in hydrogen is split by a relative amount
transition
in hydrogen is split by a relative amount
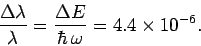 |
(1163) |
Note that this splitting is much greater than the natural line-width estimated in Eq. (1161), so there really are two spectral lines.
How does all of this affect the rate of the
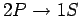 transition?
transition?
Well, we have seen that the transition rate is independent of spin, and
hence of the spin quantum number 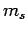 , and is
also independent of the quantum number
, and is
also independent of the quantum number 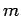 . It follows that the
transition rate is independent of the
. It follows that the
transition rate is independent of the 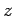 -component
of total angular momentum quantum number
-component
of total angular momentum quantum number 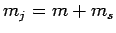 . However,
if this is the case, then the transition rate is plainly also independent of
the total angular momentum quantum number
. However,
if this is the case, then the transition rate is plainly also independent of
the total angular momentum quantum number 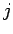 . Hence,
we expect the
. Hence,
we expect the
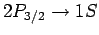 and
and
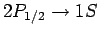 transition rates to be the same. However, there are four
transition rates to be the same. However, there are four 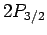 states
and only two
states
and only two 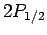 states. If these states are equally
populated--which we would certainly expect to be the case in thermal
equilibrium, since they have almost the same energies--and since they decay
to the
states. If these states are equally
populated--which we would certainly expect to be the case in thermal
equilibrium, since they have almost the same energies--and since they decay
to the 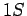 state at the same rate, it stands to reason that the
spectral line associated with the
state at the same rate, it stands to reason that the
spectral line associated with the
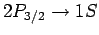 transition
is twice as bright as that associated with the
transition
is twice as bright as that associated with the
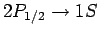 transition.
transition.



Next: Forbidden Transitions
Up: Time-Dependent Perturbation Theory
Previous: Transitions in Hydrogen
Richard Fitzpatrick
2010-07-20
![]() , and is
also independent of the quantum number
, and is
also independent of the quantum number ![]() . It follows that the
transition rate is independent of the
. It follows that the
transition rate is independent of the ![]() -component
of total angular momentum quantum number
-component
of total angular momentum quantum number ![]() . However,
if this is the case, then the transition rate is plainly also independent of
the total angular momentum quantum number
. However,
if this is the case, then the transition rate is plainly also independent of
the total angular momentum quantum number ![]() . Hence,
we expect the
. Hence,
we expect the
![]() and
and
![]() transition rates to be the same. However, there are four
transition rates to be the same. However, there are four ![]() states
and only two
states
and only two ![]() states. If these states are equally
populated--which we would certainly expect to be the case in thermal
equilibrium, since they have almost the same energies--and since they decay
to the
states. If these states are equally
populated--which we would certainly expect to be the case in thermal
equilibrium, since they have almost the same energies--and since they decay
to the ![]() state at the same rate, it stands to reason that the
spectral line associated with the
state at the same rate, it stands to reason that the
spectral line associated with the
![]() transition
is twice as bright as that associated with the
transition
is twice as bright as that associated with the
![]() transition.
transition.