

Next: Wave-Particle Duality
Up: Continuous Probability Distributions
Previous: Continuous Probability Distributions
- In the ``game'' of Russian roulette, the player inserts a single cartridge into the drum
of a revolver, leaving the other five chambers of the drum empty. The player then spins
the drum, aims at his/her head, and pulls the trigger.
- What is the probability of the player still being alive after playing the game
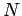 times?
times?
- What is the probability of the player surviving
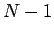 turns in this game, and then being
shot the
turns in this game, and then being
shot the 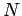 th time he/she pulls the trigger?
th time he/she pulls the trigger?
- What is the mean number of times the player gets to pull the trigger?
- Suppose that the probability density for the speed
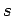 of a car on a road
is given by
of a car on a road
is given by
where
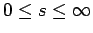 . Here,
. Here, 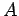 and
and 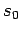 are positive constants. More
explicitly,
are positive constants. More
explicitly, 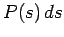 gives the probability that a car has a speed
between
gives the probability that a car has a speed
between 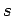 and
and 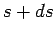 .
.
- Determine
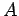 in terms of
in terms of 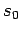 .
.
- What is the mean value of the speed?
- What is the ``most probable'' speed: i.e., the speed
for which the probability density has a maximum?
- What is the probability that a car has a speed more than three times as large
as the mean value?
- An radioactive atom has a uniform decay probability per unit time
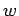 :
i.e., the probability of decay in a time interval
:
i.e., the probability of decay in a time interval 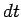 is
is 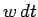 .
Let
.
Let 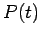 be the probability of the atom not having decayed at time
be the probability of the atom not having decayed at time 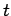 ,
given that it was created at time
,
given that it was created at time 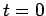 . Demonstrate that
. Demonstrate that
What is the mean lifetime of the atom?


Next: Wave-Particle Duality
Up: Continuous Probability Distributions
Previous: Continuous Probability Distributions
Richard Fitzpatrick
2010-07-20
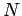 times?
times?
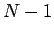 turns in this game, and then being
shot the
turns in this game, and then being
shot the 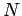 th time he/she pulls the trigger?
th time he/she pulls the trigger?
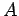 in terms of
in terms of 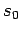 .
.