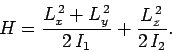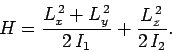Next: Central Potentials
Up: Spherical Harmonics
Previous: Spherical Harmonics
- A system is in the state
 . Calculate
. Calculate
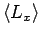 and
and
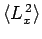 .
.
- Find the eigenvalues and eigenfunctions (in terms of the
angles
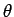 and
and 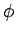 ) of
) of 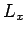 .
.
- Consider a beam of particles with
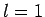 . A measurement
of
. A measurement
of 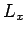 yields the result
yields the result 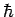 . What values will be
obtained by a subsequent measurement of
. What values will be
obtained by a subsequent measurement of 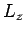 , and with what probabilities? Repeat the calculation for the cases in which the
measurement of
, and with what probabilities? Repeat the calculation for the cases in which the
measurement of 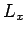 yields the results
yields the results  and
and 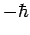 .
.
- The Hamiltonian for an axially symmetric rotator is given by
What are the eigenvalues of  ?
?
Richard Fitzpatrick
2010-07-20