


Next: Spherical Harmonics
Up: Orbital Angular Momentum
Previous: Eigenvalues of
Eigenvalues of 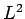
Consider the angular wavefunction
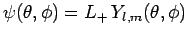 . We know that
. We know that
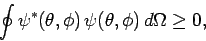 |
(576) |
since
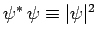 is a positive-definite real quantity.
Hence, making use of Eqs. (194) and (539), we find that
is a positive-definite real quantity.
Hence, making use of Eqs. (194) and (539), we find that
It follows from Eqs. (541), and (556)-(558) that
We, thus, obtain the constraint
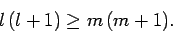 |
(579) |
Likewise, the inequality
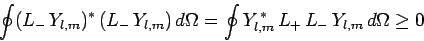 |
(580) |
leads to a second constraint:
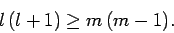 |
(581) |
Without loss of generality, we can assume that 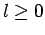 . This
is reasonable, from a physical standpoint, since
. This
is reasonable, from a physical standpoint, since
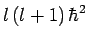 is supposed to represent the magnitude squared of something, and
should, therefore, only take non-negative values. If
is supposed to represent the magnitude squared of something, and
should, therefore, only take non-negative values. If 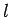 is non-negative
then the constraints (579) and (581) are equivalent
to the following constraint:
is non-negative
then the constraints (579) and (581) are equivalent
to the following constraint:
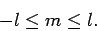 |
(582) |
We, thus, conclude that the quantum number  can only take a restricted range of integer values.
can only take a restricted range of integer values.
Well, if  can only take a restricted range of integer values then there
must exist a lowest possible value it can take. Let us call this special value
can only take a restricted range of integer values then there
must exist a lowest possible value it can take. Let us call this special value 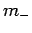 ,
and let
,
and let 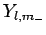 be the corresponding eigenstate. Suppose
we act on this eigenstate with the lowering operator
be the corresponding eigenstate. Suppose
we act on this eigenstate with the lowering operator 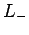 . According
to Eq. (560), this will have the effect of converting the
eigenstate into that of a state with a lower value of
. According
to Eq. (560), this will have the effect of converting the
eigenstate into that of a state with a lower value of  . However,
no such state exists. A non-existent state is represented in quantum
mechanics by the null wavefunction,
. However,
no such state exists. A non-existent state is represented in quantum
mechanics by the null wavefunction,  . Thus, we must have
. Thus, we must have
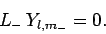 |
(583) |
Now, from Eq. (540),
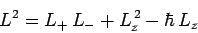 |
(584) |
Hence,
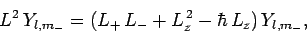 |
(585) |
or
 |
(586) |
where use has been made of (556), (557), and (583).
It follows that
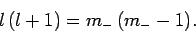 |
(587) |
Assuming that 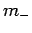 is negative, the solution to the above equation
is
is negative, the solution to the above equation
is
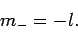 |
(588) |
We can similarly show that the largest possible value of  is
is
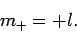 |
(589) |
The above two results imply that 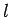 is an integer, since
is an integer, since
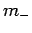 and
and 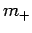 are both constrained to be integers.
are both constrained to be integers.
We can now formulate the rules which determine the allowed values
of the quantum numbers 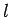 and
and  . The quantum number
. The quantum number 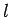 takes the non-negative integer values
takes the non-negative integer values
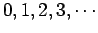 . Once
. Once
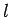 is given, the quantum number
is given, the quantum number  can take any integer value in the
range
can take any integer value in the
range
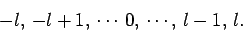 |
(590) |
Thus, if 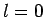 then
then  can only take the value
can only take the value  , if
, if 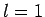 then
then
 can take the values
can take the values 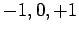 , if
, if 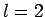 then
then  can take
the values
can take
the values 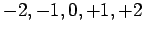 , and so on.
, and so on.



Next: Spherical Harmonics
Up: Orbital Angular Momentum
Previous: Eigenvalues of
Richard Fitzpatrick
2010-07-20

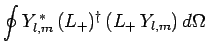
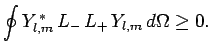
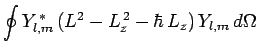
![$\displaystyle \oint Y_{l,m}^{ \ast} \hbar^2\left[l (l+1) -m (m+1)\right]Y_{l,m} d\Omega$](img1411.png)
![$\displaystyle \hbar^2 \left[l (l+1) -m (m+1)\right] \oint Y_{l,m}^{ \ast} Y_{l,m} d\Omega$](img1412.png)
![]() . This
is reasonable, from a physical standpoint, since
. This
is reasonable, from a physical standpoint, since
![]() is supposed to represent the magnitude squared of something, and
should, therefore, only take non-negative values. If
is supposed to represent the magnitude squared of something, and
should, therefore, only take non-negative values. If ![]() is non-negative
then the constraints (579) and (581) are equivalent
to the following constraint:
is non-negative
then the constraints (579) and (581) are equivalent
to the following constraint:
![]() can only take a restricted range of integer values then there
must exist a lowest possible value it can take. Let us call this special value
can only take a restricted range of integer values then there
must exist a lowest possible value it can take. Let us call this special value ![]() ,
and let
,
and let ![]() be the corresponding eigenstate. Suppose
we act on this eigenstate with the lowering operator
be the corresponding eigenstate. Suppose
we act on this eigenstate with the lowering operator ![]() . According
to Eq. (560), this will have the effect of converting the
eigenstate into that of a state with a lower value of
. According
to Eq. (560), this will have the effect of converting the
eigenstate into that of a state with a lower value of ![]() . However,
no such state exists. A non-existent state is represented in quantum
mechanics by the null wavefunction,
. However,
no such state exists. A non-existent state is represented in quantum
mechanics by the null wavefunction, ![]() . Thus, we must have
. Thus, we must have
![]() and
and ![]() . The quantum number
. The quantum number ![]() takes the non-negative integer values
takes the non-negative integer values
![]() . Once
. Once
![]() is given, the quantum number
is given, the quantum number ![]() can take any integer value in the
range
can take any integer value in the
range