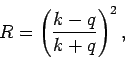Next: Multi-Particle Systems
Up: Simple Harmonic Oscillator
Previous: Simple Harmonic Oscillator
- Show that the wavefunction of a particle of mass
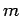 in an infinite one-dimensional square-well of width
in an infinite one-dimensional square-well of width 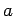 returns to its original form after a quantum revival time
returns to its original form after a quantum revival time
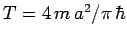 .
.
- A particle of mass
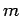 moves freely in one dimension between
impenetrable walls located at
moves freely in one dimension between
impenetrable walls located at
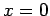 and
and 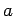 . Its initial wavefunction is
. Its initial wavefunction is
What is the subsequent time evolution of the wavefunction?
Suppose that the initial wavefunction is
What now is the subsequent time evolution? Calculate the probability
of finding the particle between 0 and 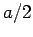 as a function of time in
each case.
as a function of time in
each case.
- A particle of mass
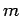 is in the ground-state of an infinite one-dimensional square-well of width
is in the ground-state of an infinite one-dimensional square-well of width 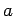 . Suddenly the well expands to
twice its original size, as the right wall moves from
. Suddenly the well expands to
twice its original size, as the right wall moves from 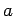 to
to 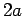 , leaving
the wavefunction momentarily undisturbed. The energy of the particle
is now measured. What is the most probable result? What is the probability
of obtaining this result? What is the next most probable result, and
what is its probability of occurrence? What is the expectation value
of the energy?
, leaving
the wavefunction momentarily undisturbed. The energy of the particle
is now measured. What is the most probable result? What is the probability
of obtaining this result? What is the next most probable result, and
what is its probability of occurrence? What is the expectation value
of the energy?
- A stream of particles of mass
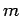 and energy
and energy 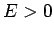 encounter a
potential step of height
encounter a
potential step of height 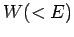 : i.e.,
: i.e., 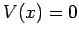 for
for 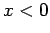 and
and
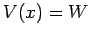 for
for 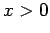 with the particles incident from
with the particles incident from 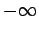 . Show that the fraction
reflected is
. Show that the fraction
reflected is
where
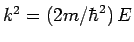 and
and
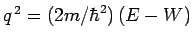 .
.
- A stream of particles of mass
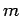 and energy
and energy 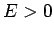 encounter the
delta-function potential
encounter the
delta-function potential
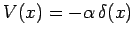 , where
, where
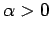 . Show that the fraction
reflected is
. Show that the fraction
reflected is
where
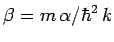 , and
, and
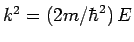 .
Does such a potential have a bound state? If so, what is its
energy?
.
Does such a potential have a bound state? If so, what is its
energy?
- Two potential wells of width
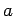 are separated by a distance
are separated by a distance 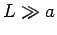 .
A particle of mass
.
A particle of mass 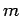 and energy
and energy 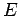 is in one of the wells. Estimate
the time required for the particle to tunnel to the other well.
is in one of the wells. Estimate
the time required for the particle to tunnel to the other well.
- Consider the half-infinite potential well
where 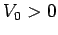 . Demonstrate that the bound-states of a particle of
mass
. Demonstrate that the bound-states of a particle of
mass 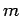 and energy
and energy 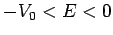 satisfy
satisfy
- Find the properly normalized first two excited energy eigenstates of
the harmonic oscillator, as well as the expectation value of the potential energy in the
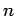 th energy eigenstate. Hint: Consider the raising and lowering operators
th energy eigenstate. Hint: Consider the raising and lowering operators 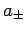 defined
in Eq. (408).
defined
in Eq. (408).



Next: Multi-Particle Systems
Up: Simple Harmonic Oscillator
Previous: Simple Harmonic Oscillator
Richard Fitzpatrick
2010-07-20