


Next: Cold Emission
Up: One-Dimensional Potentials
Previous: Square Potential Barrier
Consider a particle of mass  and energy
and energy  moving through some slowly varying
potential
moving through some slowly varying
potential 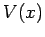 . The particle's wavefunction satisfies
. The particle's wavefunction satisfies
 |
(337) |
where
![\begin{displaymath}
k^2(x) = \frac{2 m [E-V(x)]}{\hbar^2}.
\end{displaymath}](img874.png) |
(338) |
Let us try a solution to Eq. (337) of the form
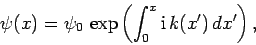 |
(339) |
where 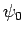 is a complex constant. Note that this solution represents
a particle propagating in the positive
is a complex constant. Note that this solution represents
a particle propagating in the positive 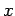 -direction [since the full
wavefunction is multiplied by
-direction [since the full
wavefunction is multiplied by
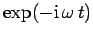 , where
, where
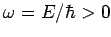 ] with the continuously varying wavenumber
] with the continuously varying wavenumber
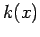 .
It follows that
.
It follows that
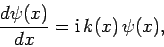 |
(340) |
and
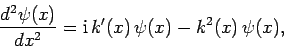 |
(341) |
where
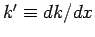 . A comparison of Eqs. (337) and (341)
reveals that Eq. (339) represents an approximate solution to
Eq. (337) provided that the first term on its right-hand side
is negligible compared to the second. This yields
the validity criterion
. A comparison of Eqs. (337) and (341)
reveals that Eq. (339) represents an approximate solution to
Eq. (337) provided that the first term on its right-hand side
is negligible compared to the second. This yields
the validity criterion 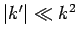 , or
, or
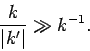 |
(342) |
In other words, the variation length-scale of 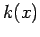 , which is
approximately the same as the variation length-scale of
, which is
approximately the same as the variation length-scale of 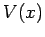 , must
be much greater than the particle's de Broglie wavelength (which
is of order
, must
be much greater than the particle's de Broglie wavelength (which
is of order  ). Let us suppose that this is the case. Incidentally,
the approximation involved in dropping the first term on the right-hand side
of Eq. (341) is generally known as the WKB approximation.
). Let us suppose that this is the case. Incidentally,
the approximation involved in dropping the first term on the right-hand side
of Eq. (341) is generally known as the WKB approximation.![[*]](footnote.png) Similarly, Eq. (339) is termed a WKB solution.
Similarly, Eq. (339) is termed a WKB solution.
According to the WKB solution (339), the probability
density remains constant: i.e.,
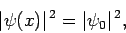 |
(343) |
as long as the particle
moves through a region in which  , and
, and 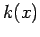 is consequently real (i.e., an allowed region
according to classical physics).
Suppose, however, that the particle encounters a potential barrier (i.e., a region from which the particle is excluded according to classical
physics). By definition,
is consequently real (i.e., an allowed region
according to classical physics).
Suppose, however, that the particle encounters a potential barrier (i.e., a region from which the particle is excluded according to classical
physics). By definition, 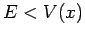 inside such a barrier, and
inside such a barrier, and
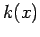 is consequently imaginary. Let the barrier extend from
is consequently imaginary. Let the barrier extend from 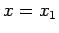 to
to 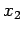 , where
, where
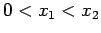 . The WKB solution inside the barrier is written
. The WKB solution inside the barrier is written
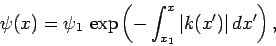 |
(344) |
where
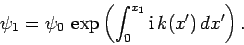 |
(345) |
Here, we have neglected the unphysical exponentially growing solution.
According to the WKB solution (344), the probability
density decays exponentially inside the barrier: i.e.,
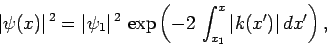 |
(346) |
where
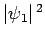 is the probability density at the left-hand
side of the barrier (i.e.,
is the probability density at the left-hand
side of the barrier (i.e., 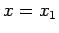 ). It follows that the
probability density at the right-hand side of the barrier (i.e.,
). It follows that the
probability density at the right-hand side of the barrier (i.e., 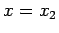 ) is
) is
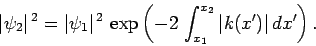 |
(347) |
Note that
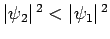 . Of course, in the region to the right of the
barrier (i.e.,
. Of course, in the region to the right of the
barrier (i.e., 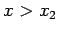 ), the probability density takes the
constant value
), the probability density takes the
constant value
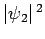 .
.
We can interpret the ratio of the probability densities to the right and to the left of the potential barrier as the probability, 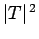 , that a particle
incident from the left will tunnel through the barrier and
emerge on the other side: i.e.,
, that a particle
incident from the left will tunnel through the barrier and
emerge on the other side: i.e.,
 |
(348) |
(see Sect. 5.3).
It is easily demonstrated that the probability of a particle incident from the
right tunneling through the barrier is the same.
Note that the criterion (342) for the validity of the WKB approximation
implies that the above transmission probability is very small. Hence,
the WKB approximation only applies to situations in which there is
very little chance of a particle tunneling through the potential barrier in question.
Unfortunately, the validity criterion (342) breaks down completely
at the edges of the barrier (i.e., at 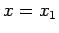 and
and 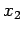 ), since
), since
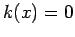 at these points. However, it can be demonstrated that the
contribution of those regions, around
at these points. However, it can be demonstrated that the
contribution of those regions, around 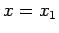 and
and 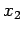 , in which the WKB
approximation breaks down to the integral in Eq. (348)
is fairly negligible. Hence, the above expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.
, in which the WKB
approximation breaks down to the integral in Eq. (348)
is fairly negligible. Hence, the above expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.



Next: Cold Emission
Up: One-Dimensional Potentials
Previous: Square Potential Barrier
Richard Fitzpatrick
2010-07-20
![[*]](footnote.png) Similarly, Eq. (339) is termed a WKB solution.
Similarly, Eq. (339) is termed a WKB solution.
![]() , that a particle
incident from the left will tunnel through the barrier and
emerge on the other side: i.e.,
, that a particle
incident from the left will tunnel through the barrier and
emerge on the other side: i.e.,
![]() and
and ![]() ), since
), since
![]() at these points. However, it can be demonstrated that the
contribution of those regions, around
at these points. However, it can be demonstrated that the
contribution of those regions, around ![]() and
and ![]() , in which the WKB
approximation breaks down to the integral in Eq. (348)
is fairly negligible. Hence, the above expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.
, in which the WKB
approximation breaks down to the integral in Eq. (348)
is fairly negligible. Hence, the above expression for the tunneling
probability is a reasonable approximation provided that the incident particle's
de Broglie wavelength is much smaller than the spatial extent of the potential
barrier.