


Next: Stationary States
Up: Fundamentals of Quantum Mechanics
Previous: Measurement
In the previous two sections, it was tacitly assumed that we were dealing
with operators possessing discrete eigenvalues and square-integrable
eigenstates. Unfortunately, some operators--most notably, 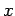 and
and
 --possess
eigenvalues which lie in a continuous range and non-square-integrable
eigenstates (in fact, these two properties go hand in hand). Let us, therefore, investigate
the eigenstates and eigenvalues of the displacement and momentum
operators.
--possess
eigenvalues which lie in a continuous range and non-square-integrable
eigenstates (in fact, these two properties go hand in hand). Let us, therefore, investigate
the eigenstates and eigenvalues of the displacement and momentum
operators.
Let  be the eigenstate of
be the eigenstate of 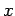 corresponding to the eigenvalue
corresponding to the eigenvalue 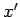 . It follows that
. It follows that
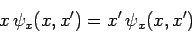 |
(277) |
for all 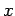 . Consider the Dirac delta-function
. Consider the Dirac delta-function  . We can write
. We can write
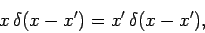 |
(278) |
since  is only non-zero infinitesimally close to
is only non-zero infinitesimally close to 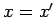 .
Evidently,
.
Evidently,  is proportional to
is proportional to  . Let us make the
constant of proportionality unity, so that
. Let us make the
constant of proportionality unity, so that
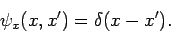 |
(279) |
Now, it is easily demonstrated that
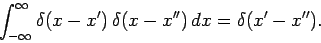 |
(280) |
Hence,  satisfies the orthonormality condition
satisfies the orthonormality condition
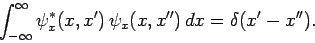 |
(281) |
This condition is analogous to the orthonormality condition (263)
satisfied by square-integrable eigenstates.
Now, by definition,  satisfies
satisfies
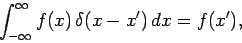 |
(282) |
where  is a general function. We can thus write
is a general function. We can thus write
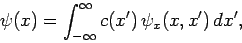 |
(283) |
where
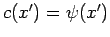 , or
, or
 |
(284) |
In other words, we can expand a general wavefunction 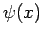 as a linear combination of the eigenstates,
as a linear combination of the eigenstates,  , of the
displacement operator. Equations (283) and (284)
are analogous to Eqs. (261) and (264), respectively,
for square-integrable eigenstates. Finally, by analogy with the
results in Sect. 4.9, the probability density of a measurement of
, of the
displacement operator. Equations (283) and (284)
are analogous to Eqs. (261) and (264), respectively,
for square-integrable eigenstates. Finally, by analogy with the
results in Sect. 4.9, the probability density of a measurement of 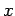 yielding the value
yielding the value 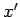 is
is 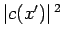 , which is equivalent to the
standard result
, which is equivalent to the
standard result
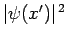 . Moreover, these probabilities are properly normalized
provided
. Moreover, these probabilities are properly normalized
provided 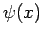 is properly normalized [cf., Eq. (265)]: i.e.,
is properly normalized [cf., Eq. (265)]: i.e.,
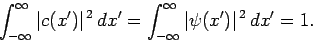 |
(285) |
Finally, if a measurement of 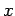 yields the value
yields the value 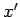 then the system
is left in the corresponding displacement eigenstate,
then the system
is left in the corresponding displacement eigenstate,  , immediately after the measurement: i.e., the wavefunction
collapses to a ``spike-function'',
, immediately after the measurement: i.e., the wavefunction
collapses to a ``spike-function'',  , as discussed in Sect. 3.16.
, as discussed in Sect. 3.16.
Now, an eigenstate of the momentum operator
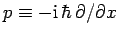 corresponding to the eigenvalue
corresponding to the eigenvalue 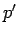 satisfies
satisfies
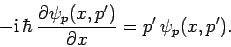 |
(286) |
It is evident that
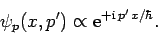 |
(287) |
Now, we require 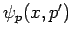 to satisfy an analogous orthonormality condition
to Eq. (281): i.e.,
to satisfy an analogous orthonormality condition
to Eq. (281): i.e.,
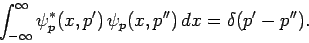 |
(288) |
Thus, it follows from Eq. (210) that the constant of proportionality
in Eq. (287) should be
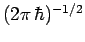 : i.e.,
: i.e.,
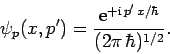 |
(289) |
Furthermore, according to Eqs. (202) and (203),
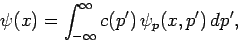 |
(290) |
where
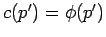 [see Eq. (203)], or
[see Eq. (203)], or
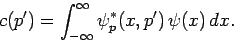 |
(291) |
In other words, we can expand a general wavefunction 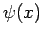 as a linear combination of the eigenstates,
as a linear combination of the eigenstates, 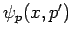 , of the
momentum operator. Equations (290) and (291)
are again analogous to Eqs. (261) and (264), respectively,
for square-integrable eigenstates. Likewise, the probability density
of a measurement of
, of the
momentum operator. Equations (290) and (291)
are again analogous to Eqs. (261) and (264), respectively,
for square-integrable eigenstates. Likewise, the probability density
of a measurement of  yielding the result
yielding the result 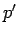 is
is 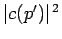 , which is equivalent to the standard result
, which is equivalent to the standard result
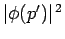 . The probabilities are also properly
normalized provided
. The probabilities are also properly
normalized provided 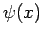 is properly normalized [cf., Eq. (221)]:
i.e.,
is properly normalized [cf., Eq. (221)]:
i.e.,
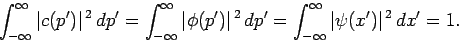 |
(292) |
Finally, if a mesurement of  yields the value
yields the value 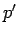 then the system
is left in the corresponding momentum eigenstate,
then the system
is left in the corresponding momentum eigenstate, 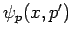 , immediately after the measurement.
, immediately after the measurement.



Next: Stationary States
Up: Fundamentals of Quantum Mechanics
Previous: Measurement
Richard Fitzpatrick
2010-07-20
![]() be the eigenstate of
be the eigenstate of ![]() corresponding to the eigenvalue
corresponding to the eigenvalue ![]() . It follows that
. It follows that
![]() corresponding to the eigenvalue
corresponding to the eigenvalue ![]() satisfies
satisfies