


Next: Helium Atom
Up: Variational Methods
Previous: Introduction
Suppose that we wish to solve the time-independent Schrödinger equation
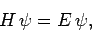 |
(1167) |
where  is a known (presumably complicated) time-independent Hamiltonian. Let
is a known (presumably complicated) time-independent Hamiltonian. Let 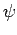 be a normalized trial solution to the above equation.
The variational principle states, quite simply, that the
ground-state energy,
be a normalized trial solution to the above equation.
The variational principle states, quite simply, that the
ground-state energy, 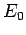 , is always less than or equal to the expectation
value of
, is always less than or equal to the expectation
value of  calculated with the trial wavefunction: i.e.,
calculated with the trial wavefunction: i.e.,
 |
(1168) |
Thus, by varying 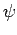 until the expectation value of
until the expectation value of  is minimized, we can
obtain an approximation to the wavefunction and energy of the ground-state.
is minimized, we can
obtain an approximation to the wavefunction and energy of the ground-state.
Let us prove the variational principle.
Suppose that the  and the
and the 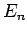 are the true eigenstates and eigenvalues
of
are the true eigenstates and eigenvalues
of  : i.e.,
: i.e.,
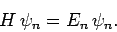 |
(1169) |
Furthermore, let
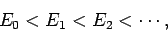 |
(1170) |
so that 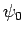 is the ground-state,
is the ground-state, 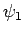 the first excited state,
etc. The
the first excited state,
etc. The  are assumed to be orthonormal:
i.e.,
are assumed to be orthonormal:
i.e.,
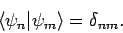 |
(1171) |
If our trial wavefunction 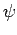 is properly normalized then
we can write
is properly normalized then
we can write
 |
(1172) |
where
 |
(1173) |
Now, the expectation value of  , calculated with
, calculated with 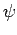 , takes the
form
, takes the
form
where use has been made of Eqs. (1169) and (1171).
So, we can write
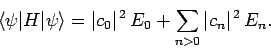 |
(1175) |
However, Eq. (1173) can be rearranged to give
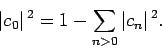 |
(1176) |
Combining the previous two equations, we obtain
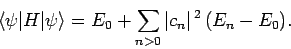 |
(1177) |
Now, the second term on the right-hand side of the above expression
is positive definite, since 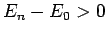 for all
for all 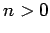 [see (1170)].
Hence, we obtain the desired result
[see (1170)].
Hence, we obtain the desired result
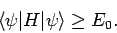 |
(1178) |
Suppose that we have found a good approximation,
 , to the ground-state
wavefunction. If
, to the ground-state
wavefunction. If 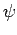 is a normalized trial wavefunction which is
orthogonal to
is a normalized trial wavefunction which is
orthogonal to
 (i.e.,
(i.e.,
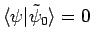 )
then, by repeating the above analysis, we can easily demonstrate that
)
then, by repeating the above analysis, we can easily demonstrate that
 |
(1179) |
Thus, by varying 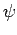 until the expectation value of
until the expectation value of  is minimized, we can
obtain an approximation to the wavefunction and energy of the first excited state. Obviously, we can continue this process until we have approximations
to all of the stationary eigenstates. Note, however, that the errors are clearly cumulative in this method,
so that any approximations to highly excited states are unlikely to be very accurate. For this reason, the variational method is generally only
used to calculate the ground-state and first few excited states of
complicated quantum systems.
is minimized, we can
obtain an approximation to the wavefunction and energy of the first excited state. Obviously, we can continue this process until we have approximations
to all of the stationary eigenstates. Note, however, that the errors are clearly cumulative in this method,
so that any approximations to highly excited states are unlikely to be very accurate. For this reason, the variational method is generally only
used to calculate the ground-state and first few excited states of
complicated quantum systems.



Next: Helium Atom
Up: Variational Methods
Previous: Introduction
Richard Fitzpatrick
2010-07-20
![]() and the
and the ![]() are the true eigenstates and eigenvalues
of
are the true eigenstates and eigenvalues
of ![]() : i.e.,
: i.e.,

![]() , to the ground-state
wavefunction. If
, to the ground-state
wavefunction. If ![]() is a normalized trial wavefunction which is
orthogonal to
is a normalized trial wavefunction which is
orthogonal to
![]() (i.e.,
(i.e.,
![]() )
then, by repeating the above analysis, we can easily demonstrate that
)
then, by repeating the above analysis, we can easily demonstrate that