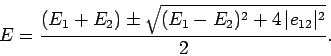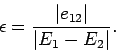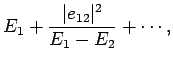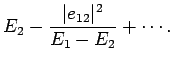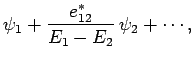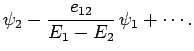Next: Non-Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Improved Notation
Consider the simplest possible non-trivial quantum mechanical system.
In such a system,
there are only two independent eigenstates
of the unperturbed Hamiltonian: i.e.,
It is assumed that these states, and their associated eigenvalues, are known.
We also expect the states to be orthonormal, and to form a complete set.
Let us now try to solve the modified energy eigenvalue problem
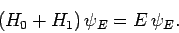 |
(877) |
We can, in fact, solve this problem exactly. Since the eigenstates
of 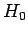 form a complete set, we can write [see Eq. (865)]
form a complete set, we can write [see Eq. (865)]
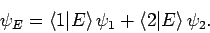 |
(878) |
It follows from (877) that
 |
(879) |
where 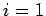 or
or 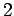 . Equations (875), (876), (878),
(879), and the orthonormality condition
. Equations (875), (876), (878),
(879), and the orthonormality condition
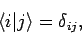 |
(880) |
yield two coupled equations which can be written
in matrix form:
![$\displaystyle \left(\begin{array}{cc}E_1-E+e_{11}& e_{12}\ [0.5ex]
e_{12}^\as...
...gle\end{array}\right)=\left(
\begin{array}{c} 0\ [0.5ex]
0\end{array}\right),$](img2128.png) |
|
|
(881) |
where
Here, use has been made of the fact that 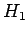 is an Hermitian operator.
is an Hermitian operator.
Consider the special (but not uncommon) case of a perturbing Hamiltonian
whose diagonal matrix elements are zero, so that
 |
(885) |
The solution of Eq. (881) (obtained by setting
the determinant of the matrix to zero) is
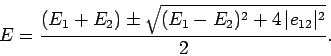 |
(886) |
Let us expand in the supposedly small parameter
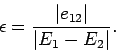 |
(887) |
We obtain
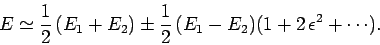 |
(888) |
The above expression yields the modification of the
energy eigenvalues due to the perturbing Hamiltonian:
Note that 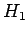 causes the upper eigenvalue to rise, and the lower to fall.
It is easily demonstrated that the modified eigenstates take the form
causes the upper eigenvalue to rise, and the lower to fall.
It is easily demonstrated that the modified eigenstates take the form
Thus, the modified energy eigenstates consist of one of the
unperturbed eigenstates, plus a slight admixture of the other.
Now our expansion procedure is only valid when 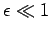 .
This suggests that the condition for the validity of the perturbation
method as a whole is
.
This suggests that the condition for the validity of the perturbation
method as a whole is
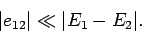 |
(893) |
In other words, when we say that 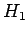 needs to be small compared to
needs to be small compared to
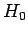 , what we are really saying is that the above inequality must be
satisfied.
, what we are really saying is that the above inequality must be
satisfied.



Next: Non-Degenerate Perturbation Theory
Up: Time-Independent Perturbation Theory
Previous: Improved Notation
Richard Fitzpatrick
2010-07-20