


Next: Improved Notation
Up: Time-Independent Perturbation Theory
Previous: Time-Independent Perturbation Theory
Consider the following very commonly occurring problem. The Hamiltonian of a
quantum mechanical system is written
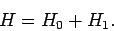 |
(854) |
Here, 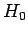 is a simple Hamiltonian whose eigenvalues and eigenstates
are known exactly.
is a simple Hamiltonian whose eigenvalues and eigenstates
are known exactly. 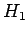 introduces some interesting additional
physics into the problem, but is sufficiently complicated that when
we add it to
introduces some interesting additional
physics into the problem, but is sufficiently complicated that when
we add it to 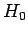 we can no longer find the exact energy eigenvalues
and eigenstates. However,
we can no longer find the exact energy eigenvalues
and eigenstates. However, 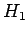 can, in some sense (which we shall
specify more precisely later on), be regarded as being small compared
to
can, in some sense (which we shall
specify more precisely later on), be regarded as being small compared
to 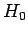 . Can we find approximate eigenvalues and eigenstates
of the modified Hamiltonian,
. Can we find approximate eigenvalues and eigenstates
of the modified Hamiltonian, 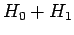 , by performing some
sort of perturbation expansion about the eigenvalues and eigenstates of the original
Hamiltonian,
, by performing some
sort of perturbation expansion about the eigenvalues and eigenstates of the original
Hamiltonian, 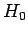 ? Let us investigate.
? Let us investigate.
Incidentally, in this chapter, we shall only discuss so-called time-independent
perturbation theory, in which the modification to the Hamiltonian,
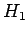 , has no explicit dependence on time. It is also assumed
that the unperturbed Hamiltonian,
, has no explicit dependence on time. It is also assumed
that the unperturbed Hamiltonian, 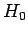 , is time-independent.
, is time-independent.
Richard Fitzpatrick
2010-07-20
![]() , has no explicit dependence on time. It is also assumed
that the unperturbed Hamiltonian,
, has no explicit dependence on time. It is also assumed
that the unperturbed Hamiltonian, ![]() , is time-independent.
, is time-independent.