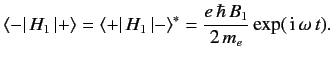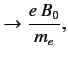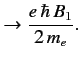Next: Dyson Series
Up: Time-Dependent Perturbation Theory
Previous: Two-State System
Consider a bound electron placed in a
uniform  -directed magnetic field, and then subjected to a small time-dependent magnetic field rotating in the
-directed magnetic field, and then subjected to a small time-dependent magnetic field rotating in the  -
- plane.
Thus,
plane.
Thus,
![$\displaystyle {\bf B} = B_0\, {\bf e}_z + B_1\left[\cos(\omega\, t) \,{\bf e}_x + \sin(\omega \,t) \,{\bf e}_y\right],$](img1833.png) |
(765) |
where 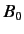 and
and  are constants, with
are constants, with
 . The rotating magnetic
field usually represents the magnetic component of an
electromagnetic wave propagating along the
. The rotating magnetic
field usually represents the magnetic component of an
electromagnetic wave propagating along the  -axis. In this system, the
electric component of the wave has no effect.
The Hamiltonian is written
-axis. In this system, the
electric component of the wave has no effect.
The Hamiltonian is written
where
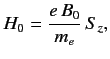 |
(767) |
and
![$\displaystyle H_1 = \frac{e\, B_1}{m_e} \left[\cos(\omega\, t) \,S_x + \sin(\omega\, t)\, S_y\right].$](img1838.png) |
(768) |
The eigenstates of the unperturbed Hamiltonian are the `spin up' and
`spin down' states, denoted 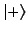 and
and 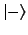 , respectively.
Thus,
, respectively.
Thus,
 |
(769) |
The time-dependent Hamiltonian can be written
![$\displaystyle H_1 = \frac{e\, B_1}{2 \,m_e} \left[\exp(\,{\rm i}\,\omega \,t)\, S^- + \exp(-{\rm i}\,\omega\, t)\, S^+\right],$](img1841.png) |
(770) |
where
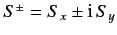 are the conventional raising and lowering operators
for spin angular momentum. It follows that
are the conventional raising and lowering operators
for spin angular momentum. It follows that
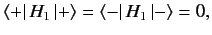 |
(771) |
and
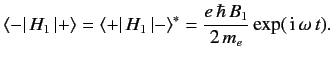 |
(772) |
It can be seen that this system is exactly the same as the two-state system
discussed in the previous section, provided that we make the identifications
The resonant frequency,
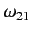 , is simply the spin precession frequency
for an electron in a uniform magnetic field of strength
, is simply the spin precession frequency
for an electron in a uniform magnetic field of strength 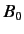 . In the
absence of the perturbation, the expectation values of
. In the
absence of the perturbation, the expectation values of 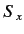 and
and 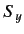 oscillate because of the spin precession, but the expectation value
of
oscillate because of the spin precession, but the expectation value
of 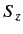 remains invariant. If we now apply a magnetic perturbation rotating
at the resonant frequency then, according to the analysis of the previous
section, the system undergoes a succession of spin-flops,
remains invariant. If we now apply a magnetic perturbation rotating
at the resonant frequency then, according to the analysis of the previous
section, the system undergoes a succession of spin-flops,
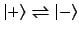 , in addition to the spin
precession. We also know that if the oscillation frequency of the
applied field is very different from the resonant frequency then there is
virtually zero probability of the field triggering a spin-flop. The width
of the resonance (in frequency) is determined by the strength of the
oscillating magnetic perturbation. Experimentalist are able to measure the
magnetic moments of electrons, and other spin one-half particles, to a
high degree of accuracy by placing the particles in a magnetic field,
and subjecting them to an oscillating magnetic field whose frequency is
gradually scanned.
By determining the resonant frequency (i.e., the frequency at which the
particles absorb energy from the oscillating field), it is possible to
calculate the magnetic moment.
, in addition to the spin
precession. We also know that if the oscillation frequency of the
applied field is very different from the resonant frequency then there is
virtually zero probability of the field triggering a spin-flop. The width
of the resonance (in frequency) is determined by the strength of the
oscillating magnetic perturbation. Experimentalist are able to measure the
magnetic moments of electrons, and other spin one-half particles, to a
high degree of accuracy by placing the particles in a magnetic field,
and subjecting them to an oscillating magnetic field whose frequency is
gradually scanned.
By determining the resonant frequency (i.e., the frequency at which the
particles absorb energy from the oscillating field), it is possible to
calculate the magnetic moment.



Next: Dyson Series
Up: Time-Dependent Perturbation Theory
Previous: Two-State System
Richard Fitzpatrick
2013-04-08
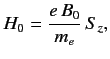
![$\displaystyle H_1 = \frac{e\, B_1}{m_e} \left[\cos(\omega\, t) \,S_x + \sin(\omega\, t)\, S_y\right].$](img1838.png)
![]() and
and ![]() , respectively.
Thus,
, respectively.
Thus,

![$\displaystyle H_1 = \frac{e\, B_1}{2 \,m_e} \left[\exp(\,{\rm i}\,\omega \,t)\, S^- + \exp(-{\rm i}\,\omega\, t)\, S^+\right],$](img1841.png)