


Next: Two-State System
Up: Time-Independent Perturbation Theory
Previous: Time-Independent Perturbation Theory
We have developed techniques by which the general energy eigenvalue problem
can be reduced to a set of coupled partial differential equations involving
various wavefunctions. Unfortunately, the number of such problems that yield
exactly soluble equations is comparatively small. It is, therefore, necessary to develop techniques for finding
approximate solutions to otherwise intractable problems.
Consider the following problem, which is very common. The Hamiltonian of a
system is written
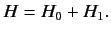 |
(583) |
Here, 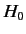 is a simple Hamiltonian for which we know
the exact eigenvalues and eigenstates.
is a simple Hamiltonian for which we know
the exact eigenvalues and eigenstates. 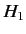 introduces some
interesting additional physics into the problem, but it is sufficiently
complicated that when we add it to
introduces some
interesting additional physics into the problem, but it is sufficiently
complicated that when we add it to 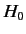 we can no longer find the exact
energy eigenvalues and eigenstates. However,
we can no longer find the exact
energy eigenvalues and eigenstates. However, 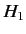 can, in some sense
(which we shall specify more exactly later on), be regarded as
being small compared to
can, in some sense
(which we shall specify more exactly later on), be regarded as
being small compared to 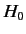 . Let us try to find approximate eigenvalues
and eigenstates of the modified Hamiltonian,
. Let us try to find approximate eigenvalues
and eigenstates of the modified Hamiltonian, 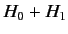 , by performing a perturbation analysis about the eigenvalues
and eigenstates of the original Hamiltonian,
, by performing a perturbation analysis about the eigenvalues
and eigenstates of the original Hamiltonian, 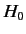 .
.



Next: Two-State System
Up: Time-Independent Perturbation Theory
Previous: Time-Independent Perturbation Theory
Richard Fitzpatrick
2013-04-08