


Next: Analysis
Up: Addition of Angular Momentum
Previous: Addition of Angular Momentum
Consider a hydrogen atom whose orbiting electron is in an 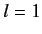 state. The electron, consequently,
possesses orbital angular momentum of magnitude
state. The electron, consequently,
possesses orbital angular momentum of magnitude 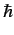 , and spin angular
momentum of magnitude
, and spin angular
momentum of magnitude 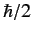 . So, what is the electron's total angular momentum?
. So, what is the electron's total angular momentum?
Richard Fitzpatrick
2013-04-08