


Next: Uncertainty Relation
Up: Fundamental Concepts
Previous: Degeneracy
Suppose that we wish to
simultaneously measure two observables,  and
and  , of a
microscopic system? Let us assume that we possess an apparatus that is
capable of measuring
, of a
microscopic system? Let us assume that we possess an apparatus that is
capable of measuring  , and another that can measure
, and another that can measure  . For instance,
the two observables in question might be the projection in the
. For instance,
the two observables in question might be the projection in the
 - and
- and  -directions of the
spin angular momentum of a spin one-half particle. These could be measured using
appropriate Stern-Gerlach apparatuses (see Sakurai, Section 1.1).
Suppose that we make a measurement of
-directions of the
spin angular momentum of a spin one-half particle. These could be measured using
appropriate Stern-Gerlach apparatuses (see Sakurai, Section 1.1).
Suppose that we make a measurement of  , and the system is
consequently thrown into
one of the eigenstates of
, and the system is
consequently thrown into
one of the eigenstates of  ,
,
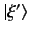 , with eigenvalue
, with eigenvalue  . What
happens if we now make a measurement of
. What
happens if we now make a measurement of  ? Well, suppose that
the eigenstate
? Well, suppose that
the eigenstate
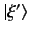 is also an eigenstate of
is also an eigenstate of  , with eigenvalue
, with eigenvalue
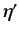 . In this case, a measurement of
. In this case, a measurement of  will definitely give the
result
will definitely give the
result 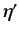 . A second measurement of
. A second measurement of  will definitely give the
result
will definitely give the
result  , and so on. In this sense, we can say that
the observables
, and so on. In this sense, we can say that
the observables  and
and  simultaneously have the values
simultaneously have the values  and
and 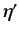 , respectively.
Clearly, if all eigenstates of
, respectively.
Clearly, if all eigenstates of  are also eigenstates of
are also eigenstates of  then
it is always possible to make a simultaneous measurement of
then
it is always possible to make a simultaneous measurement of  and
and  .
Such observables are termed compatible.
.
Such observables are termed compatible.
Suppose, however, that the eigenstates of  are not eigenstates of
are not eigenstates of  .
Is it still possible to measure both observables simultaneously? Let us again
make an observation of
.
Is it still possible to measure both observables simultaneously? Let us again
make an observation of  which throws the system into an eigenstate
which throws the system into an eigenstate
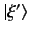 , with eigenvalue
, with eigenvalue  .
We can now make a second observation to determine
.
We can now make a second observation to determine  .
This will throw the system into one of the (many) eigenstates of
.
This will throw the system into one of the (many) eigenstates of  which
depend on
which
depend on
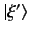 . In principle, each of these eigenstates is
associated with a different result of the measurement. Suppose that the
system is thrown into an eigenstate
. In principle, each of these eigenstates is
associated with a different result of the measurement. Suppose that the
system is thrown into an eigenstate
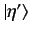 , with the eigenvalue
, with the eigenvalue 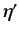 .
Another measurement of
.
Another measurement of  will throw the system into one of the (many)
eigenstates of
will throw the system into one of the (many)
eigenstates of  which depend on
which depend on
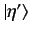 .
Each eigenstate is again associated with a different possible
result of the measurement. It is clear that if the observables
.
Each eigenstate is again associated with a different possible
result of the measurement. It is clear that if the observables
 and
and  do not possess simultaneous eigenstates then if the value
of
do not possess simultaneous eigenstates then if the value
of  is known (i.e., the system is in an eigenstate of
is known (i.e., the system is in an eigenstate of  ) then the
value of
) then the
value of  is uncertain (i.e., the system is not in an eigenstate
of
is uncertain (i.e., the system is not in an eigenstate
of  ), and vice versa. We say that the two observables are
incompatible.
), and vice versa. We say that the two observables are
incompatible.
We have seen that the condition for two observables  and
and  to
be simultaneously measurable is that they should possess simultaneous
eigenstates (i.e., every eigenstate of
to
be simultaneously measurable is that they should possess simultaneous
eigenstates (i.e., every eigenstate of  should also be an eigenstate
of
should also be an eigenstate
of  ). Suppose that this is the case. Let a general eigenstate of
). Suppose that this is the case. Let a general eigenstate of
 , with eigenvalue
, with eigenvalue  , also be an eigenstate of
, also be an eigenstate of
 , with eigenvalue
, with eigenvalue 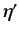 . It is convenient to denote this
simultaneous eigenstate
. It is convenient to denote this
simultaneous eigenstate
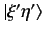 . We have
. We have
We can left-multiply the first equation by  , and the second equation
by
, and the second equation
by  , and then take the difference. The result is
, and then take the difference. The result is
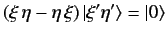 |
(65) |
for each simultaneous eigenstate.
Recall that the eigenstates of an observable must form a complete set. It follows
that the simultaneous eigenstates of two observables must also form a complete set.
Thus, the above equation implies that
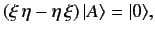 |
(66) |
where  is a general ket. The only way that this can
be true is if
is a general ket. The only way that this can
be true is if
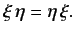 |
(67) |
Thus, the condition for two observables  and
and  to be simultaneously
measurable is that they should commute.
to be simultaneously
measurable is that they should commute.



Next: Uncertainty Relation
Up: Fundamental Concepts
Previous: Degeneracy
Richard Fitzpatrick
2013-04-08
![]() are not eigenstates of
are not eigenstates of ![]() .
Is it still possible to measure both observables simultaneously? Let us again
make an observation of
.
Is it still possible to measure both observables simultaneously? Let us again
make an observation of ![]() which throws the system into an eigenstate
which throws the system into an eigenstate
![]() , with eigenvalue
, with eigenvalue ![]() .
We can now make a second observation to determine
.
We can now make a second observation to determine ![]() .
This will throw the system into one of the (many) eigenstates of
.
This will throw the system into one of the (many) eigenstates of ![]() which
depend on
which
depend on
![]() . In principle, each of these eigenstates is
associated with a different result of the measurement. Suppose that the
system is thrown into an eigenstate
. In principle, each of these eigenstates is
associated with a different result of the measurement. Suppose that the
system is thrown into an eigenstate
![]() , with the eigenvalue
, with the eigenvalue ![]() .
Another measurement of
.
Another measurement of ![]() will throw the system into one of the (many)
eigenstates of
will throw the system into one of the (many)
eigenstates of ![]() which depend on
which depend on
![]() .
Each eigenstate is again associated with a different possible
result of the measurement. It is clear that if the observables
.
Each eigenstate is again associated with a different possible
result of the measurement. It is clear that if the observables
![]() and
and ![]() do not possess simultaneous eigenstates then if the value
of
do not possess simultaneous eigenstates then if the value
of ![]() is known (i.e., the system is in an eigenstate of
is known (i.e., the system is in an eigenstate of ![]() ) then the
value of
) then the
value of ![]() is uncertain (i.e., the system is not in an eigenstate
of
is uncertain (i.e., the system is not in an eigenstate
of ![]() ), and vice versa. We say that the two observables are
incompatible.
), and vice versa. We say that the two observables are
incompatible.
![]() and
and ![]() to
be simultaneously measurable is that they should possess simultaneous
eigenstates (i.e., every eigenstate of
to
be simultaneously measurable is that they should possess simultaneous
eigenstates (i.e., every eigenstate of ![]() should also be an eigenstate
of
should also be an eigenstate
of ![]() ). Suppose that this is the case. Let a general eigenstate of
). Suppose that this is the case. Let a general eigenstate of
![]() , with eigenvalue
, with eigenvalue ![]() , also be an eigenstate of
, also be an eigenstate of
![]() , with eigenvalue
, with eigenvalue ![]() . It is convenient to denote this
simultaneous eigenstate
. It is convenient to denote this
simultaneous eigenstate
![]() . We have
. We have