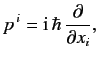

Next: Dirac Equation
Up: Relativistic Electron Theory
Previous: Relativistic Electron Theory
The aim of this chapter is to develop a quantum mechanical theory of electron
dynamics that is consistent with special relativity. Such a theory is needed
to explain the origin of electron spin (which is essentially a relativistic effect),
and to account for the fact that the spin contribution to the electron's magnetic
moment is twice what we would naively expect by analogy with (non-relativistic)
classical physics (see Section 5.5). Relativistic electron theory is
also required to fully understand the fine structure of the hydrogen
atom energy levels (recall, from Section 7.7, and Exercises 3 and 4, that the modification to the energy
levels due to spin-orbit coupling is of the same order of magnitude as the
first-order correction due to the electron's relativistic mass increase.)
In the following, we shall use
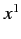 ,
, 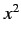 ,
, 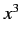 to represent the Cartesian coordinates
to represent the Cartesian coordinates 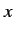 ,
, 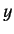 ,
, 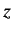 , respectively, and
, respectively, and 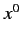 to represent
to represent 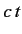 .
The time dependent wavefunction then takes the form
.
The time dependent wavefunction then takes the form
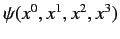 . Adopting
standard relativistic notation, we write the four
. Adopting
standard relativistic notation, we write the four 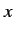 's as
's as 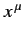 , for
, for
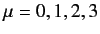 . A space-time
vector with four components that transforms under Lorentz transformation in an analogous manner to the four space-time coordinates
. A space-time
vector with four components that transforms under Lorentz transformation in an analogous manner to the four space-time coordinates
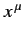 is termed a 4-vector, and its components are written like
is termed a 4-vector, and its components are written like 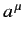 (i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
(i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
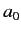 |
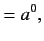 |
(1098) |
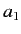 |
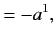 |
(1099) |
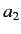 |
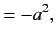 |
(1100) |
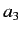 |
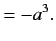 |
(1101) |
Here, the 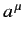 are called the contravariant components of the vector
are called the contravariant components of the vector 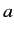 , whereas the
, whereas the
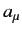 are termed the covariant components. Two 4-vectors
are termed the covariant components. Two 4-vectors 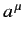 and
and 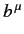 have the Lorentz invariant scalar product
have the Lorentz invariant scalar product
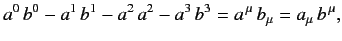 |
(1102) |
a summation being implied over a repeated letter suffix. The metric tenor
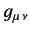 is defined
is defined
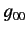 |
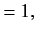 |
(1103) |
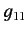 |
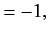 |
(1104) |
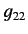 |
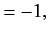 |
(1105) |
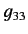 |
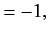 |
(1106) |
with all other components zero.
Thus,
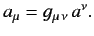 |
(1107) |
Likewise,
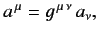 |
(1108) |
where 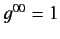 ,
,
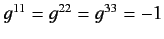 , with all other components zero.
Finally,
, with all other components zero.
Finally,
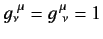 if
if 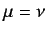 , and
, and
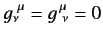 otherwise.
otherwise.
In the Schrödinger representation, the momentum of a particle, whose components are written 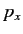 ,
, 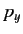 ,
, 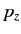 , or
, or 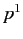 ,
, 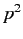 ,
, 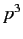 ,
is represented by the operators
,
is represented by the operators
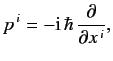 |
(1109) |
for 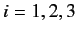 . Now, the four operators
. Now, the four operators
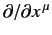 form the covariant components of a
4-vector whose contravariant components are written
form the covariant components of a
4-vector whose contravariant components are written
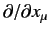 . So, to make
expression (1109) consistent with relativistic theory, we must first write it with its
suffixes balanced,
. So, to make
expression (1109) consistent with relativistic theory, we must first write it with its
suffixes balanced,
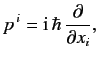 |
(1110) |
and then extend it to the complete 4-vector equation
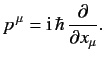 |
(1111) |
According to standard relativistic theory, the new operator
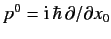 , which forms a 4-vector when
combined with the momenta
, which forms a 4-vector when
combined with the momenta 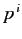 , is interpreted as the energy of the particle divided by
, is interpreted as the energy of the particle divided by 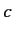 , where
, where 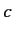 is the velocity of
light in vacuum.
is the velocity of
light in vacuum.


Next: Dirac Equation
Up: Relativistic Electron Theory
Previous: Relativistic Electron Theory
Richard Fitzpatrick
2013-04-08
![]() ,
, ![]() ,
, ![]() to represent the Cartesian coordinates
to represent the Cartesian coordinates ![]() ,
, ![]() ,
, ![]() , respectively, and
, respectively, and ![]() to represent
to represent ![]() .
The time dependent wavefunction then takes the form
.
The time dependent wavefunction then takes the form
![]() . Adopting
standard relativistic notation, we write the four
. Adopting
standard relativistic notation, we write the four ![]() 's as
's as ![]() , for
, for
![]() . A space-time
vector with four components that transforms under Lorentz transformation in an analogous manner to the four space-time coordinates
. A space-time
vector with four components that transforms under Lorentz transformation in an analogous manner to the four space-time coordinates
![]() is termed a 4-vector, and its components are written like
is termed a 4-vector, and its components are written like ![]() (i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
(i.e., with an upper
Greek suffix). We can lower the suffix according to the rules
![]() ,
, ![]() ,
, ![]() , or
, or ![]() ,
, ![]() ,
, ![]() ,
is represented by the operators
,
is represented by the operators