


Next: General Analysis
Up: Time-Dependent Perturbation Theory
Previous: Time-Dependent Perturbation Theory
Suppose that the Hamiltonian of a given quantum mechanical system
can be written
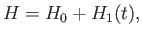 |
(8.1) |
where the unperturbed Hamiltonian, 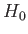 , does not depend on time explicitly, and
, does not depend on time explicitly, and 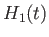 is a small
time-dependent perturbation. In the following, it is assumed that we are able to calculate
the eigenkets and eigenvalues of the unperturbed Hamiltonian exactly. These are denoted
is a small
time-dependent perturbation. In the following, it is assumed that we are able to calculate
the eigenkets and eigenvalues of the unperturbed Hamiltonian exactly. These are denoted
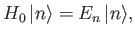 |
(8.2) |
where 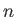 is an integer.
We know that if the system is initially in one of the
eigenstates of
is an integer.
We know that if the system is initially in one of the
eigenstates of 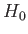 then, in the absence of the external
perturbation, it remains in that state for ever. (See Section 3.5.) However,
the presence of a small time-dependent perturbation can, in principle,
give rise to a finite probability that a system initially in some
eigenstate
then, in the absence of the external
perturbation, it remains in that state for ever. (See Section 3.5.) However,
the presence of a small time-dependent perturbation can, in principle,
give rise to a finite probability that a system initially in some
eigenstate 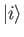 of the unperturbed Hamiltonian
is found in some other eigenstate at a subsequent time (because
of the unperturbed Hamiltonian
is found in some other eigenstate at a subsequent time (because
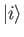 is no longer an exact eigenstate of the total
Hamiltonian).
In other words,
a time-dependent perturbation allows
the system to make transitions between
its unperturbed energy eigenstates. Let us investigate such transitions.
is no longer an exact eigenstate of the total
Hamiltonian).
In other words,
a time-dependent perturbation allows
the system to make transitions between
its unperturbed energy eigenstates. Let us investigate such transitions.



Next: General Analysis
Up: Time-Dependent Perturbation Theory
Previous: Time-Dependent Perturbation Theory
Richard Fitzpatrick
2016-01-22